Discrete Sets in Geometry

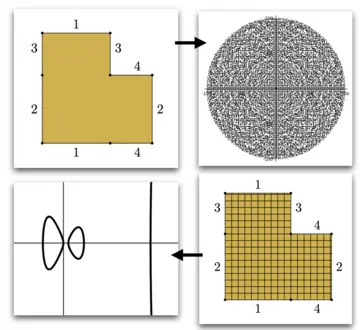
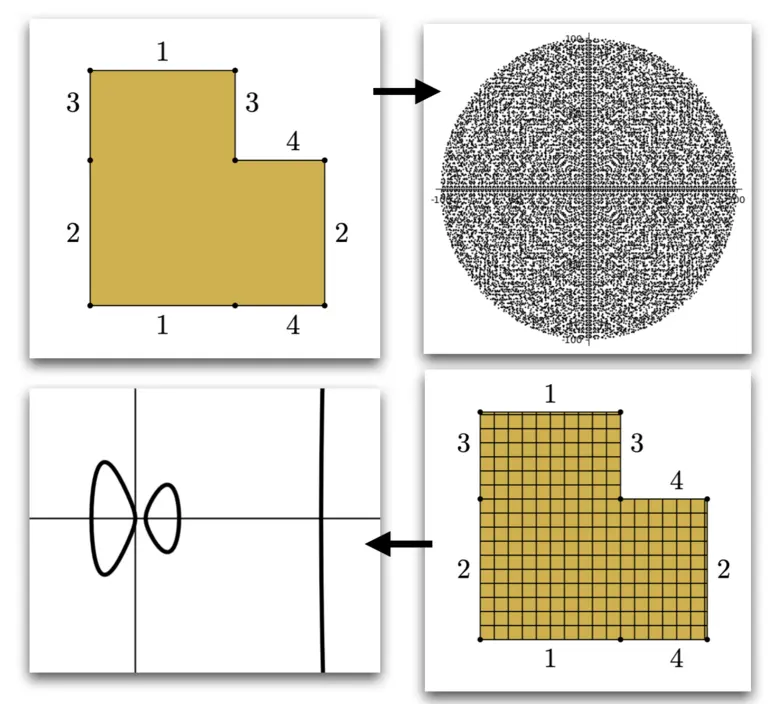
The geometric objects of focus are Riemann surfaces, specifically those written as translation surfaces formed by gluing sides of polygons. Discrete sets arising from Riemann surfaces include sets of geodesics, or sampling points on a Riemann surface in order to approximate the algebraic curve. In the first case, number theory and dynamics play a large role in the techniques of study. In the latter, we delve into ideas about how to cross the Transcendental Divide, which requires the use of transcendental functions to directly move between Riemann surfaces and Algebraic Curves. Along the way, we have to learn varieties from sample points, giving connections to data science.