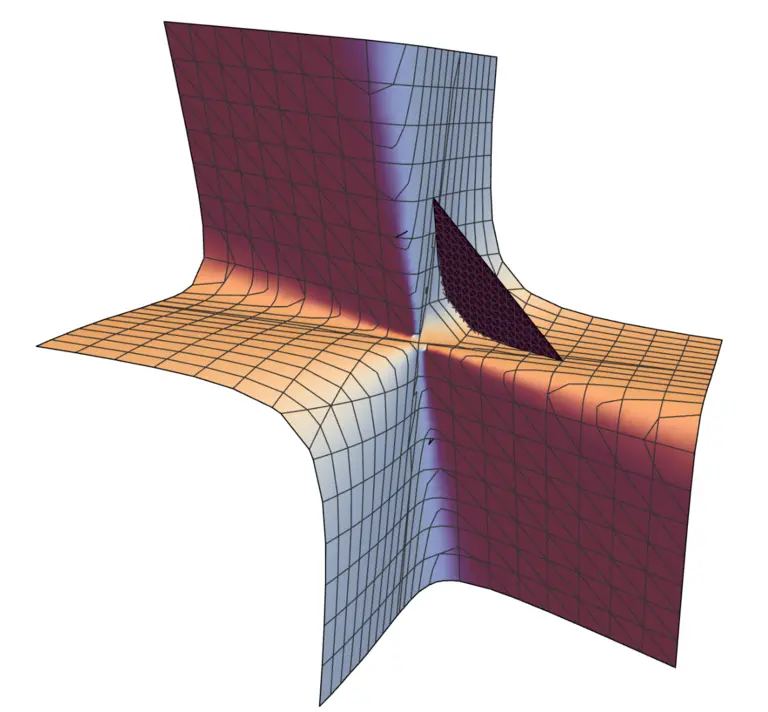
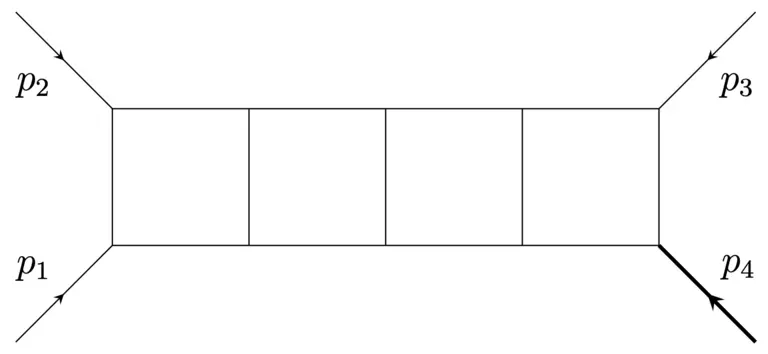
Algebraic Analysis

Numerous important functions in real-world applications are holonomic, i.e., they are solutions to certain systems of linear differential equations with polynomial coefficients. A typical example of such functions are observables in dependency of time or position, such as the displacement of an oscillating ukulele string. Holonomic functions are ubiquitous in the sciences: among them are many trigonometric functions, hypergeometric functions, some probability distributions, cosmological correlation functions, and many more.

Observations in physical experiments often suggest and initiate new mathematical rules. Our group aims to set up these exciting mathematical structures in a self-contained manner. Application wise, we put a particular focus on Feynman integrals which are a key ingredient for the investigation of scattering processes of elementary particles. We investigate these Mellin integrals via suitable cohomology theories for algebraic varieties, and match approaches from different scientific areas. We are also interested in applying algebraic geometry to data-related topics of fundamental nature, such as maximum likelihood estimation, topological data analysis, or the structure of function spaces in the theory of artificial neural networks.