Algebraic Analysis
Algebraic analysis tackles linear differential equations and their solution functions by means of algebraic geometry. We are concerned with the concise study of these equations and explore further algebraic structures behind important functions in the sciences. We put a particular focus on Feynman integrals.
Research
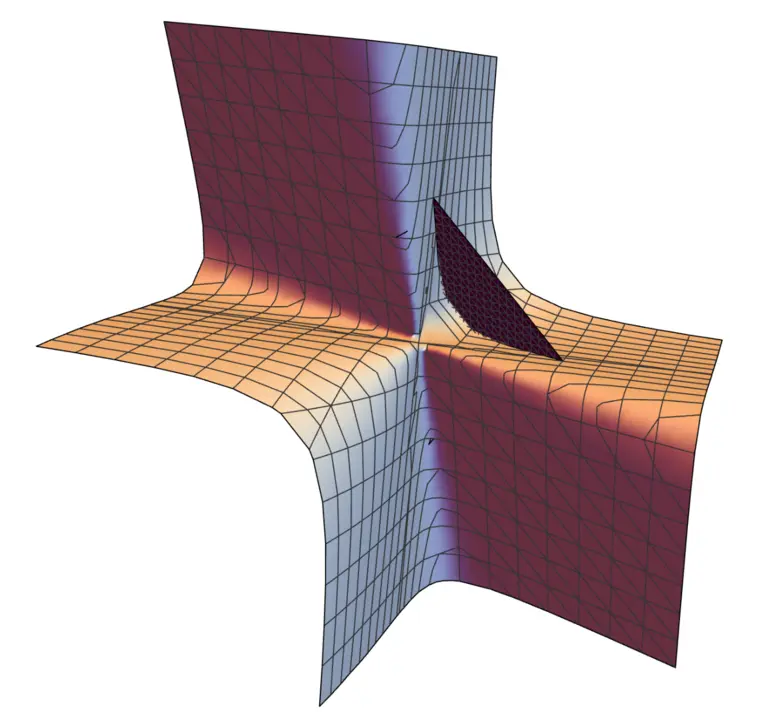
Numerous important functions in real-world applications are holonomic, i.e., they are solutions to certain systems of linear differential equations with polynomial coefficients. A typical example of such functions are observables in dependency of time or position, such as the displacement of an oscillating ukulele string. Holonomic functions are ubiquitous in the sciences: among them are many trigonometric functions, hypergeometric functions, some probability distributions, cosmological correlation functions, and many more.
Algebraically, one encodes such PDEs as elements of the Weyl algebra — a non-commutative ring, denoted D. Passing from a function to its annihilating D-ideal has several advantages. First of all, one can read crucial properties of a function from its annihilating D-ideal. Moreover, one can manipulate the function itself through symbolic computations with the D-ideal. The mathematical field of algebraic analysis not only allows for structural insights into the nature of linear PDE but also for new computational approaches such as the algorithmic computation of series solutions to D-ideals.
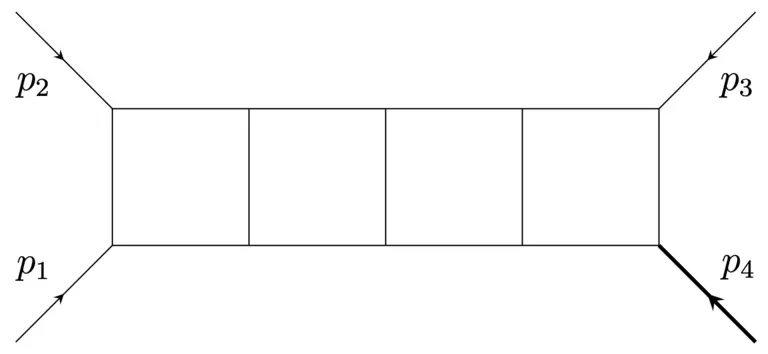
Observations in physical experiments often suggest and initiate new mathematical rules. Our group aims to set up these exciting mathematical structures in a self-contained manner. Application wise, we put a particular focus on Feynman integrals which are a key ingredient for the investigation of scattering processes of elementary particles. We investigate these Mellin integrals via suitable cohomology theories for algebraic varieties, and match approaches from different scientific areas. We are also interested in applying algebraic geometry to data-related topics of fundamental nature, such as maximum likelihood estimation, topological data analysis, or the structure of function spaces in the theory of artificial neural networks.
This group is part of UNIVERSE+, funded by the European Union (ERC, UNIVERSE PLUS, 101118787). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.