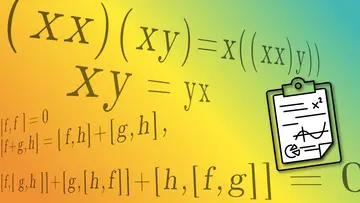Kohomologische Feldtheorien sichern erfolgreiche Dissertation

Glückwünsche gebühren auch Shuhan Jiang zur erfolgreichen Verteidigung seiner Dissertation. Er ist Forscher in der Gruppe von Jürgen Jost, der seine hervorragende Arbeit über „Mathematische Strukturen kohomologischer Feldtheorien“ betreut hat. Für die Zukunft wünschen wir alles Gute!

Shuhan Jiang erwarb seinen Bachelor of Science in Physik an der Nankai Universität in China. 2018 wurde er als Predoctoral Fellow Mitglied der Forschungsgruppe „Geometrie, Analysis, Theoretische Physik und Maschinelles Lernen“ unter der Leitung unseres Direktors Jürgen Jost. Seine aktuellen Forschungsinteressen umfassen gradierte Geometrie und kohomologische Feldtheorie. Zuvor arbeitete er auch auf dem Gebiet der Quanteninformationstheorie, insbesondere an der Bell'schen Nichtlokalität, Mehrfachverschränkungen und der Quanteninformatik.

Konkret beschreibt er seine Forschung wie folgt (in Englisch): „In this dissertation, we developed a mathematical framework for cohomological field theories (CohFTs) in the language of ‘QK-manifolds’, which unifies the previous ones in (Baulieu and Singer 1988; Baulieu and Singer 1989; Ouvry, Stora, and Van Baal 1989; Atiyah and Jeffrey 1990; Birmingham et al. 1991; Kalkman 1993; Blau 1993). Within this new framework, we classified the (gauge invariant) solutions to the descent equations in CohFTs (with gauge symmetries). We revisited Witten’s idea of topological twisting and showed that the twisted super-Poincaré algebra gives rise naturally to a ‘QK-structure’. We also generalized the Mathai-Quillen construction of the universal Thom class via a variational bicomplex lift of the equivariant cohomology. Our framework enables a uniform treatment of examples like topological quantum mechanics, topological sigma model, and topological Yang-Mills theory.“