Nonlinear Algebra - Tropical Geometry
Tropical geometry is a mathematical theory that connects algebraic and discrete geometry through the study of tropical varieties. The process of tropicalization allows for the degeneration of an algebraic variety to a skeleton that can be studied using techniques from discrete geometry and combinatorics. Tropical methods have been applied in enumerative algebraic geometry and moduli spaces of curves, and have also led to new insights in optimization, machine learning, game theory, statistics, physics, and biology.
Introduction
Tropical geometry is a recent mathematical theory that connects algebraic and discrete geometry. The objects studied in tropical geometry are tropical varieties. Tropical varieties are finite unions of polyhedra that are stacked well, namely, so that two polyhedra touch at a face that is common to both. Similarly to their algebraic counterparts, they are defined by conditions imposed by tropical polynomials. Tropical geometry allows one to speak of degeneration of an algebraic variety via a process called tropicalization, which is a formal mathematical tool that associates a tropical variety to a given algebraic one. Intuitively, we can think of this as a limit process that shrinks the algebraic variety to its skeleton. This skeleton retains essential information of the original variety and it can now be studied using new techniques and methods for discrete geometry and combinatorics.
Tropical methods have been successfully applied in enumerative algebraic geometry to count how many curves of a certain type pass through a given number of points, and in the theory of moduli spaces of curves that describes all possible different curves of a given type. At the same time, they have brought new perspective on research in discrete geometry and combinatorics. This has led to the establishment of tropical geometry as an active area of research in its own right, which is at the core of our research group at the Max Planck Institute for Mathematics in the Sciences.
Algebraic aspects of tropical geometry first appeared in applied areas of mathematics. The establishment of the tropical geometric theory has nourished the interactions of geometry with different areas of mathematics. Tropical geometry has been recently used in optimization, machine learning, game theory, statistics, physics and biology, bringing new geometric insights to these areas.
Moduli space of abstract tropical curves
An abstract tropical curve is a connected graph with edge-lengths and vertex decorations that satisfy certain stability conditions. They are dual graphs to nodal singular algebraic curves. Figure 1 shows an example of the combinatorial type of a tropical curve, i.e., the underlying graph without the edge-length information, with genus three and two marked points. The moduli spaces $\Delta_{g,n}$ of abstract tropical curves are topological spaces that parametrize tropical curves of genus $g$ with $n$ marked points. They are constructed like a simplicial complex but with possibly quotients of standard simplices. These moduli spaces have very interesting combinatorial and topological structures. For example, the space $\Delta_{0,5}$ is the Petersen graph, see Figure 2.
The tropical moduli spaces are closely connected to the classical algebraic moduli spaces $\mathcal{M}_{g,n}$ of curves of genus $g$ with $n$ marked points. In fact, the rational homology of $\Delta_{g,n}$ can be identified with one piece in the rational cohomology of $\mathcal{M}_{g,n}$. That way, we transfer the hard question of studying cohomology of $\mathcal{M}_{g,n}$ to the question of studying the topology and combinatorics of a cell complex.
Tropical differential algebra
An algebraic (ordinary) differential equation is an equation given as the vanishing of a polynomial in the variables $x,x',x^{(2)}, x^{(3)} \dots$. As an example, the equation \[ x' - x = 0 \] has the exponential power series $\sum_{n=0}^\infty t^n/n!$ as solution.
In analogy to tropical geometry, Grigoriev introduced a way to tropicalize algebraic ODEs with coefficients in a power series ring $K[\![t]\!]$, recording only a \emph{first order} information. When the field $K$ of coefficients is trivially valued, solutions to such tropical ODEs are Boolean power series satisfying certain combinatorial constraints.
The aim is to recover information about the classical solutions by computing the tropical ones.
All classical solutions tropicalize to tropical ones, but do all tropical solutions lift? As in classical tropical geometry, this is an instance of a fundamental theorem, that has been proven by Aroca et al. and Fink-Toghani for trivial valuation on $K$. These techniques can also be applied to PDEs, and a fundamental theorem (proved by Falkensteiner et al.), holds in this context too.
Recently, the framework developed by Grigoriev has been extended to the non-trivially valued case, opening up the possibility of application in the world of number theory.
Here is another tropical question on PDEs: given a $p$-adic differential equation, is it possible to compute its irregularity or the convergence radii of its solutions via tropical methods?
Bergman fans
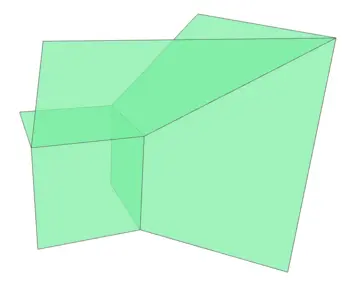
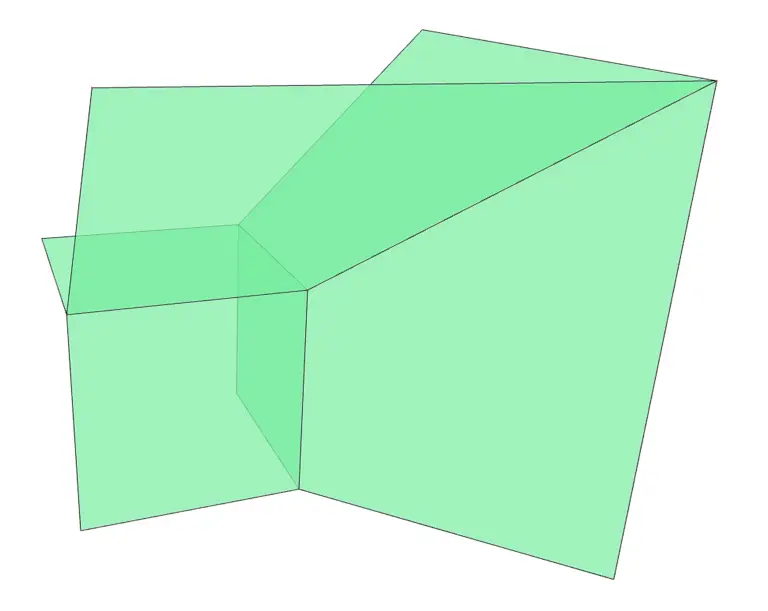
Tropical varieties come in all shapes and forms, but locally they always look like Bergman fans.
This is reminiscent to manifolds, where locally they look like linear spaces.
So what is a Bergman fan?
Given a matroid $M = (E, \mathcal B)$, we can assign weights to $E$ in such a way that for each circuit, the weight in the circuit does not have a unique minimum.
This tropical condition allows for a description of a matroid as a tropical variety:
$$\Sigma_M = \{ \vec{x} \in \mathbb{R}^E | \min_{c\in \mathcal C} x_c \text{ is attained at least twice}\}.$$
Its face structure is related to the flats of the matroid.
Being a matroid invariant, the Bergman fan is used in studying chromatic invariants of matroids.
In 2013, Eric Katz and June Huh used the Bergman fan to prove Rota's conjecture.
Interesting mathematics arises in Bergman fans when we consider piecewise polynomial functions on the support of this fan.
These functions form a ring, related to the Chow ring of the matroid.
The degree of the Bergman fan of a matroid has important meaning in matroid theory: it is its beta invariant.
Algorithms to compute the intersection of Bergman fans with generic fans have been developed to compute this degree explicitly.
The tropical Grassmannian
The classical algebraic Grassmannian is a standard example of a parameter space: A point in the Grassmannian ${\rm Gr}(k,n)$ is a linear subspace of $K^n$ of dimension $k$. For example, ${\rm Gr}(1,2) \cong \mathbb{P}^1$ is the space of lines in the plane that pass through the origin.
Tropicalizing the Grassmannian gives rise to the parameter space of all realizable tropical linear spaces, also called tropicalized linear spaces. However, it is also possible to define tropical linear spaces without using algebraic linear spaces and tropicalization. With this approach we can recover all tropicalized linear spaces, but we also obtain tropical linear spaces that cannot be realized by algebraic linear spaces. The parameter space of these more general tropical linear spaces is the Dressian, a tropical prevariety which contains the tropical Grassmannian as a subvariety.
These spaces have a strong connection to matroid theory, as a point in the Dressian can be interpreted as a valuated matroid, and Bergman fans are special tropical linear spaces.
The setting of the tropical Grassmannian also has connections to other areas: for example, the tropical Grassmannian ${\rm trop}({\rm Gr}(2,n))$ is equivalent to the space of phylogenetic trees with $n$ leaves. These trees appear in biology as models of the evolutionary connections between species.