Optimal transport
Optimal transportation
Optimal transportation describes the problem of finding the most efficient way to move distribution of materials
... and optimal matching
A common problem in these applications is to have two sets of data points
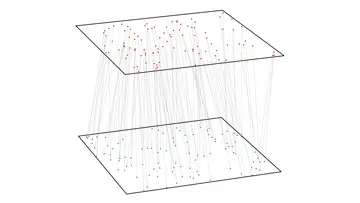
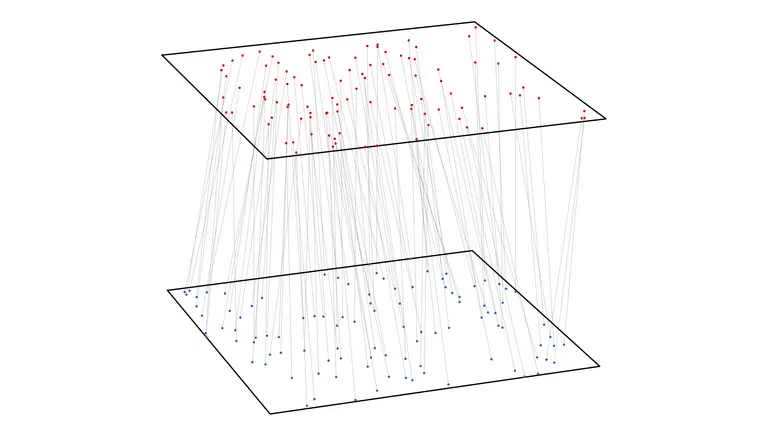
An illustration of such a matching, where both
As shown in (2) fluctuations are effective in low dimension, exhibiting a logarithmic correction when
Optimal matchings in 2d
Note that the optimal matching problem as described in (1) can be seen as a special case of optimal transportation problems where the original and final distributions are point measures, that is they are discrete measures. Indeed, defining
This allows to study (1) from an analytical point of view exploiting the rich structure of optimal transport combining tools from convex analysis and partial differential equations. In [7] a very precise ansatz regarding convergence of the re-scaled cost in dimension
So far, we have focused on the matching problem on large scales. Thus we are interested in matching infinite point clouds in the whole space
Harmonic approximation
The proof of the non-existence of stationary, locally optimal matchings in 2d is based on a tool, which is called harmonic approximation. It says that optimal transportation maps are well-approximated by harmonic maps.
The harmonic approximation result was originally developed in [13], in order to study the regularity properties of solutions to the quadratic optimal transportation problem. These problems had been studied before mainly using techniques from nonlinear PDE theory developed by Caffarelli. The outcome of these studies was a partial
This approach relies primarily on the connection of the optimal transportation problem with a lineari\ed PDE problem. Note that we can view an optimal transportation map
It turns out that not only does the change of variables formula hold, but
The idea of the harmonic approximation is to perform a Taylor-expansion for around the identity. Since


If this argument is not just formal, but can be made rigorous, we should expect that
Regularity results for continuous densities were obtained in [12], while the boundary case was treated in [22]
More general cost funtions
The aforementioned regularity results can be extended to cost functions that locally look like the Euclidean cost function
Multi-marginal
A natural generalization of the optimal transport problem is the question of optimally coupling more than two measures, leading to the so-called multi-marginal optimal transport problem. Multi-marginal optimal transport, originally considered by Gangbo and Święch [11], has recently received attention due to its connection to barycenters of measures with respect to the Wasserstein geometry [1], which provides a natural way of interpolating many probability measures. However, the regularity properties of this interpolating density is far from being well-understood. If the cost function is given by pairwise Coulomb interaction, the multi-marginal optimal transport problem also arises as a semi-classical limit (in the strong coupling regime) of electronic density functional theory [8]. Due to the repulsive nature of the cost, the behavior of optimal transport in this case is rather different from the usually considered cost functions and many questions remain open.
References
Agueh, M. and Carlier, G., Barycenters in the Wasserstein space. SIAM Journal on Mathematical Analysis 43 (2011), 904–924.
Ajtai, M., Komlós, J. and Tusnády, G., On optimal matchings. Combinatorica 4 (1984), 259–264.
Ambrosio, L., Stra, F. and Trevisan, D., A PDE approach to a 2-dimensional matching problem. Probability Theory and Related Fields 173 (1) (2019), 433–477.
Ambrosio, L., Glaudo F., and Trevisan, D., On the optimal map in the 2-dimensional random matching problem. Discrete and Continuous Dynamical Systems 39(12) (2019), 7291–7308.
Ambrosio, L., Goldman, M. and Trevisan, D., On the quadratic random matchingproblem in two-dimensional domains.
Borda, B., Empirical measures and random walks on compact spaces in the quadratic Wasserstein metric. arXiv preprint arXiv:2110.00295 (2021).
Caracciolo, S., Lucibello, C., Parisi, G. and Sicuro, G., Scaling hypothesis for the Euclidean bipartite matching problem. Physical Review E 90(1) (2015), 012118.
Cotar, C., Friesecke, G., C. Klüppelberg, Smoothing of transport plans with fixed marginals and rigorous semiclassical limit of the Hohenberg–Kohn functional. Arch. Ration. Mech. Anal. 228 (2018), 891–922.
De Philippis, G., and Figalli, A., Partial regularity for optimal transport maps. Publications Mathématiques. Institut de Hautes Études Scientifiques 121 (2015), 81–112.
Figalli, A. and Kim, Y.-H., Partial regularity of Brenier solutions of the Monge–Ampère equation. Discrete Contin. Dyn. Syst. 28:2 (2010), 559–565.
Gangbo, W. and Święch, A., Optimal Maps for the Multidimensional Monge-Kantorovich Problem. Communications on Pure and Applied Mathematics LI (1998), 23–45.
Goldman, M., An epsilon-regularity result for optimal transport maps between continuous densities. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 31:4 (2020), 971–979.
Goldman, M. and Otto, F., A variational proof of partial regularity for optimal transportation maps. Ann. Sci. Ec. Norm. Super. 53:5 (2020).
Goldman, M., Huesmann, M. and Otto, F., Quantitative linearization results for the Monge–Ampère equation. Commun. Pure Appl. Math 74:12 (2021), 2483–2560.
Goldman M. and Huesmann M., A fluctuation result for the displacement in the optimal matching problem. Ann. Probab. 50(4) (2022), 1446-1477.
Goldman, M. and Trevisan, D., Convergence of asymptotic costs for random Euclidean matching problems. accepted in Prob. and Math. Phy (2022)
Goldman, M. and Trevisan, D. Optimal transport methods for combinatorial optimization over two random point sets.
Jalowy, J. The Wasserstein distance to the Circular Law. Annales de l’Institut Henri Poincaré, Probabilités et Statistiques, to appear (2023).
Huesmann, M., Mattesini, F. and Otto, F., There is no stationary cyclically monotone Poisson matching in 2d.
Huesmann, H., Mattesini, F. and Trevisan, D. Wasserstein asymptotics for the empirical measure of fractional Brownian motion on a flat torus. Stochastic Processes and their Applications 155 (2023), 1–26.
Mézard, M. and Parisi, G., The Euclidean matching problem. J. Phys. France 49(12) (1988), 2019-2025.
Miura, T. and Otto, F., Sharp boundary ε-regularity of optimal transport maps. Adv. Math. 381:107603 (2021).
Otto, F., Prod’homme, M. and Ried, T. Variational approach to regularity of optimal transport maps : general cost functions. Ann. PDE 7:2 (2021).
Santambrogio, F., Optimal transport for Applied Mathematicians. Birkhäuser Cham (2015).
Villani, C., Optimal Transport. Old and new. Springer Berlin, Heidelberg (2009).
Wang, F.-Y., Precise limit in Wasserstein distance for conditional empirical measures of Dirichlet diffusion processes. Journal of Functional Analysis 280 (2021), 108998.