Frobenius structures, Operads, Deformation Theory & Applications (F-sODA)

This group aims at developing and exploring new bridges between domains of algebraic geometry, algebraic topology, and information geometry. As it has been shown in [1], there is a deep interplay between these fundamental domains, that have until now evolved independently. Our aim is to investigate new unexpected paths, within these areas of mathematics.

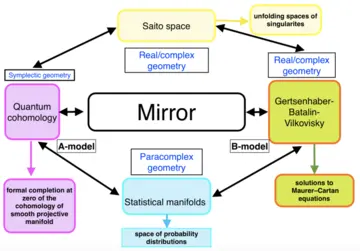
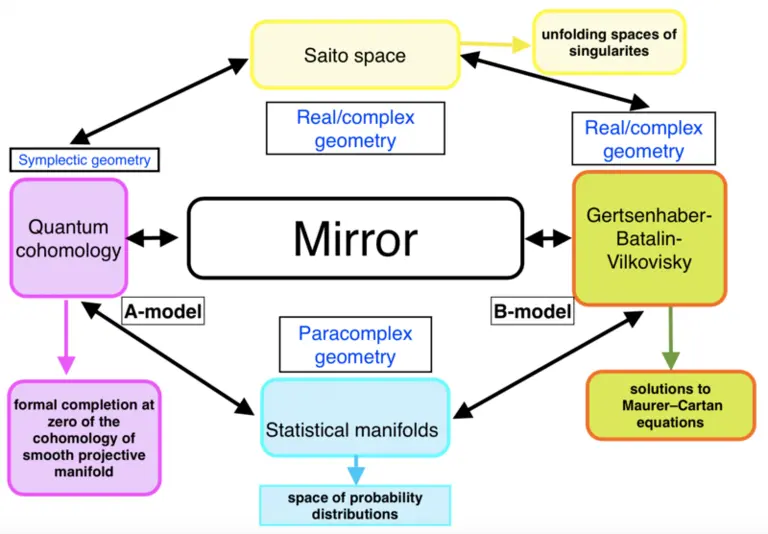
In the recent work of N. Combe & Yu. Manin from 2020 (see [1]), there was an important discovery of a very unexpected bridge connecting algebraic geometry and the domain of probabilities and statistics, via the notion of Frobenius manifolds.

Frobenius manifolds are mathematical objects that arose in the process of axiomatization of Topological Field Theory.

Until 2020, three main classes of Frobenius manifolds were listed (and roughly presented) as:

1. Quantum cohomology, in relation to Gromov--Witten invariants,
2. Saito manifold (unfolding spaces of singularities), in relation to Landau--Ginzburg models,
3. The moduli space of solutions to Maurer--Cartan equations appearing in the Barannikov--Kontsevich theory.

It has been proved in [1] that this list of Frobenius manifolds is not exhaustive and that there exists an unexpected fourth class: the class of statistical manifolds.

Statistical manifolds play a central role in geometry of information, decision theory, and machine learning. However, this object has a very rich geometry and algebraic interpretation.

Based on this viewpoint, an important task in this research program is to understand the underlying algebraic and geometric structures, which are hidden within the Frobenius manifolds, and to understand their mechanisms.

Considering the richness of the interaction of these classes of Frobenius manifolds, we also explore their ramifications to other domains of mathematics, such as the Grothendieck—Teichmüller theory (see [2]).