The Ubiquity of Linear Orders in Combinatorics

One common technique in the study of structures associated to a finite set is to enrich them with a total order and study the additionally acquired properties. This occurs frequently in mathematics, oftentimes implicitly. For instance, a collection of vectors on ${\mathbb{R}}^n$ can be arranged as the columns of a matrix. Often, the order of these columns matters a great deal. For example, solving very large linear systems underlies much of scientific computing, and choosing a good column order can make the difference between a usable solution and complete failure. Even in theoretical situations where you may think order plays no role, it can provide additional structure worth studying.

By abstracting the notion of linear independence one encounters matroids: objects originally defined by Whitney to study graphs and vector configurations. Matroids have found a place in numerous applications to pure and applied mathematics. Roughly speaking, one forgets about coordinates but remembers which vectors are linearly independent. This allows us to better understand the topology of hyperplane arrangements, torus orbits in Grassmannians, the success of greedy algorithms, and more, purely in terms of combinatorics. In all these examples, much of the combinatorial analysis relies heavily on the choice of linear order.

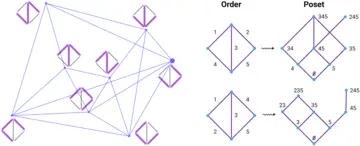
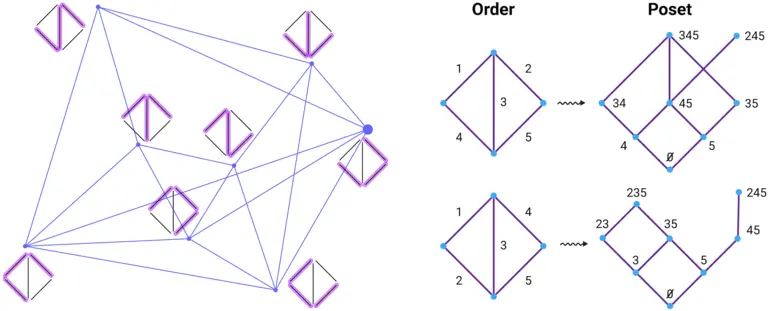
One advantage of passing to the language of matroids is that many questions can be recast in terms of polytopes and simplicial complexes, which have rich combinatorial and geometric structure. Of particular interest to us are shelling orders; inductive recipes to build these combinatorial objects in a way that easily keeps track of some important changes occurring along the way. The importance of constructing matroids by using shelling orders has long been recognized, but the dependence on the specific order has not been fully exploited.