
Former Research Group - Minerva Group
Spectral Hypergraph Theory
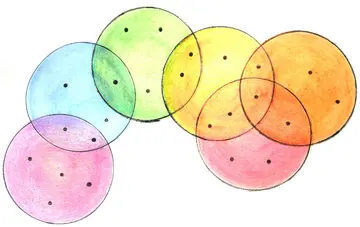
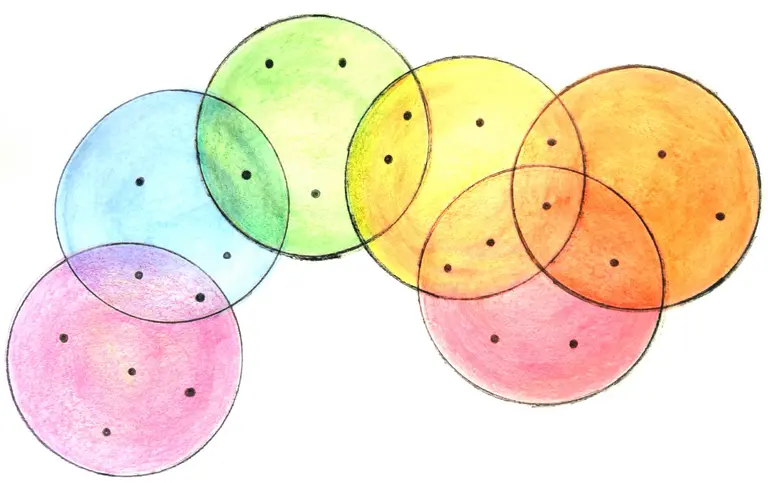
A hypergraph with six hyperedges
Spectral hypergraph theory studies the qualitative properties of a hypergraph that can be inferred from the eigenvalues and the eigenvectors of either square matrices or tensors associated with it. It generalizes the spectral theory of graphs, which has a long history and is widely used in applications.
Research topics in this area include, but are not limited to:
- Spectra of given hypergraphs
- Relations between the spectra of hypergraphs and their structural properties
- Eigenvalue bounds
- Spectral classes
- Algorithmic aspects
- Applications to dynamical systems and applications to data analysis of empirical networks (e.g. biological and chemical networks)
/
Publications
inJournal
2025At the end of the spectrum : chromatic bounds for the largest eigenvalue of the normalized Laplacian
In: Journal of physics : complexityinJournal
2024A measure-theoretic representation of graphs
In: Periodica mathematica HungaricainJournal
2024Maximal colourings for graphs
In: Graphs and combinatoricsinJournal
2024There is no going back : Properties of the non-backtracking Laplacian
In: Linear algebra and its applicationsinJournal
2024Exploring the space of graphs with fixed discrete curvatures
In: Journal of physics : complexityPreprint
2023Uniform density in matroids, matrices and graphs
inJournal
2023Petals and books : the largest Laplacian spectral gap from 1
In: Journal of graph theoryinJournal
2023Spectral theory of the non-backtracking Laplacian for graphs
In: Discrete mathematicsinJournal
2023Interview with László Lovász
In: EMS magazineinJournal
2023On Turán numbers for disconnected hypergraphs
In: Acta mathematica hungaricainJournal
2022Signless normalized Laplacian for hypergraphs
In: Electronic journal of graph theory and applicationsinJournal
2022Coupled hypergraph maps and chaotic cluster synchronization
In: eplinJournal
2022
In: Vietnam journal of mathematics
inJournal
2022Spectral gap of the largest eigenvalue of the normalized graph Laplacian
In: Communications in mathematics and statisticsinJournal
2022Stochastic rotating waves
In: Stochastics and dynamicsinBook
2022Graphs, simplicial complexes and hypergraphs : spectral theory and topology
In: Higher-order systemsinJournal
2022Random walks and Laplacians on hypergraphs : When do they match?
In: Discrete applied mathematicsinJournal
2022Star complements for ±2 in signed graphs
In: Special matricesinJournal
2022The Aleph of Borges and the paradise of Cantor
In: Journal of humanistic mathematicsinJournal
2022The classical limit and spontaneous symmetry breaking in algebraic quantum theory
In: Expositiones mathematicae
/