Logo Max-Planck-Institute for Mathematics in the Sciences, Go to Homepage
Search
Login
Group

Cluster Algebras

Cluster algebras are structures that lie at the interface of algebra and combinatorics which appear in surprising ways throughout mathematics. We answer fundamental questions about cluster algebras by investigating the interaction between their algebraic and combinatorial structure.

Research

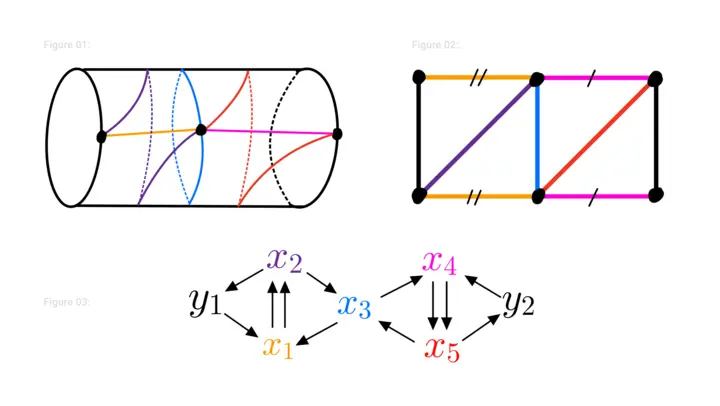
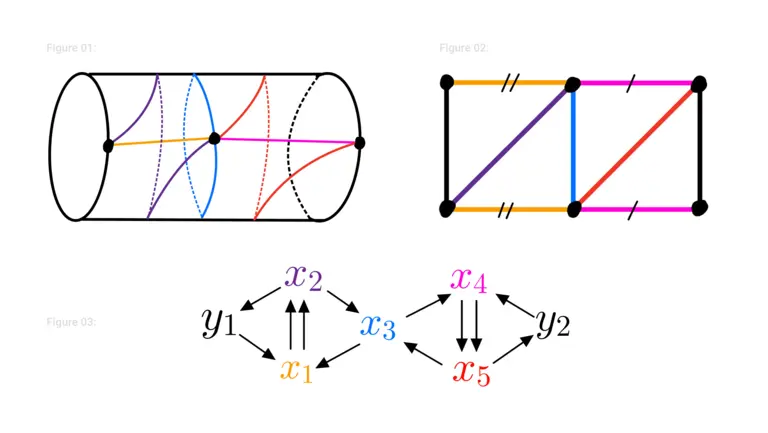
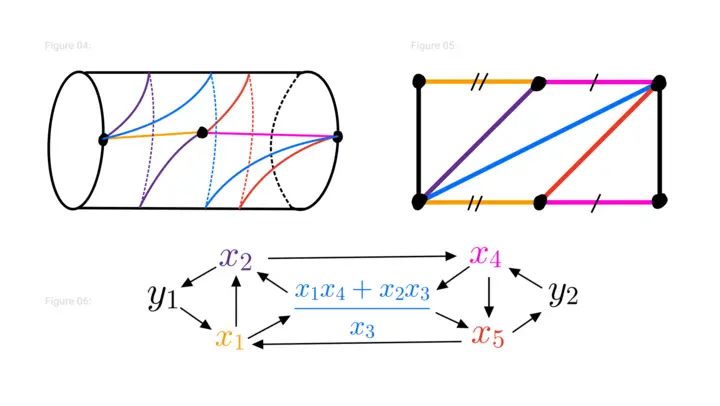
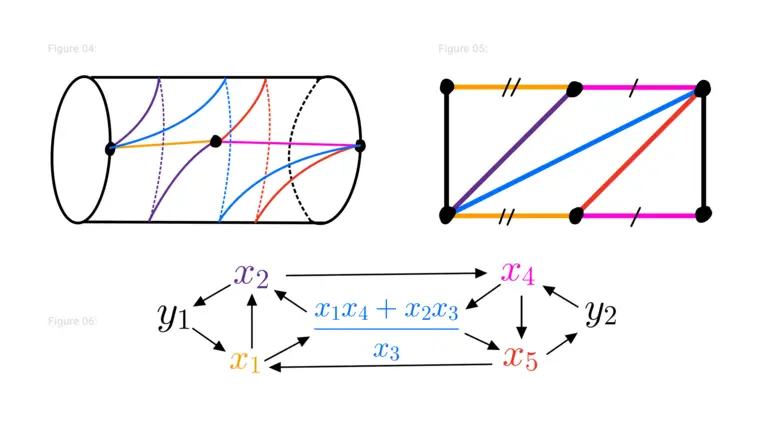
Cluster Algebras are algebras which are “grown” by starting with a seed and mutating it to produce new seeds. The combinatorics of seeds and their mutations are directly a generalization of the combinatorics of triangulations of surfaces and flips of triangulation. Figures 1, 2, 3  shows a triangulation of a punctured annulus and the associated seed in a cluster algebra. Mutation of this seed corresponds to changing the triangulation by a “flip” which removes an arc and replaces it with the unique new arc which forms a new triangulation. Figures 4, 5, 6 show a new triangulation and associated mutated seed which arises as a flip at the blue arc in the centre.

Triangulation of a punctured annulus and the associated seed in a cluster algebra
New triangulation and associated mutated seed
Triangulation of a punctured annulus and the associated seed in a cluster algebra (Figure 1, 2, 3) New triangulation and associated mutated seed (Figure 4, 5, 6)
/

We can visualize all of the mutations and seeds together via the exchange graph, shown for this example in Figure 7. The nodes of this graph are the seeds of the cluster algebra and the edges are the mutations. The colors of the nodes encode the combinatorial type of the triangulation each seed corresponds to. 

The power of these algebras often comes when one can realize some complicated algebraic transformation as a sequence of cluster mutations. One example of this is the action of the mapping class group on the decorated Teichmüller space of a surface; the action of a mapping class can be realized as a sequence of flips of triangulations which in turn can be realized as a sequence of cluster mutations. For more general cluster algebras there is a generalization of the mapping class group which acts on them called the “Cluster Modular Group”, which again acts as sequences of mutations. This group is essentially the symmetry group of the exchange graph, in Figure 7, the cluster modular group acts by translation symmetries of the graph. 

Our group is interested in the following kinds of questions:

  • How can we compute the cluster modular group of a general cluster algebra?
  • How does a general cluster modular group compare to the mapping class group of a surface?
  • Can we understand the action of the cluster modular group on the cluster algebra itself? What are the associated invariants?
  • How can we define and understand non-commutative analogs of these algebras inspired from Higher Teichmüller theory?
Figure 07: All mutations and seeds together
All mutations and seeds together (Figure 07)

Members

Publications

Not yet available

The group does not have any publications at this time.