New mathematical tools for studying particle collisions

A collaboration between the mathematicians Claudia Fevola, Simon Telen and the physicist Sebastian Mizera paves the way to more accurate predictions in the Standard Model of particle physics. Their results have just been published in Physical Review Letters.

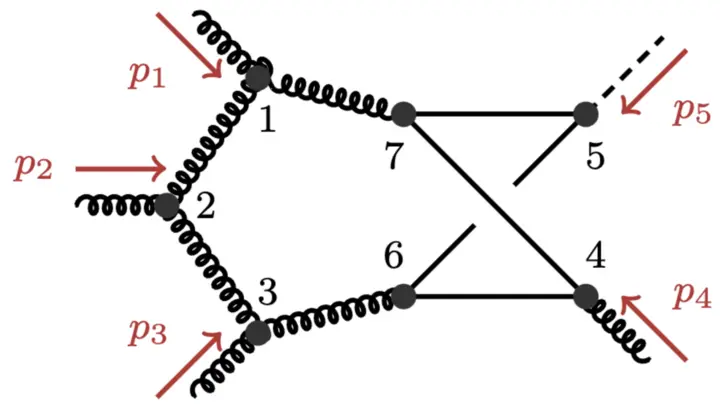
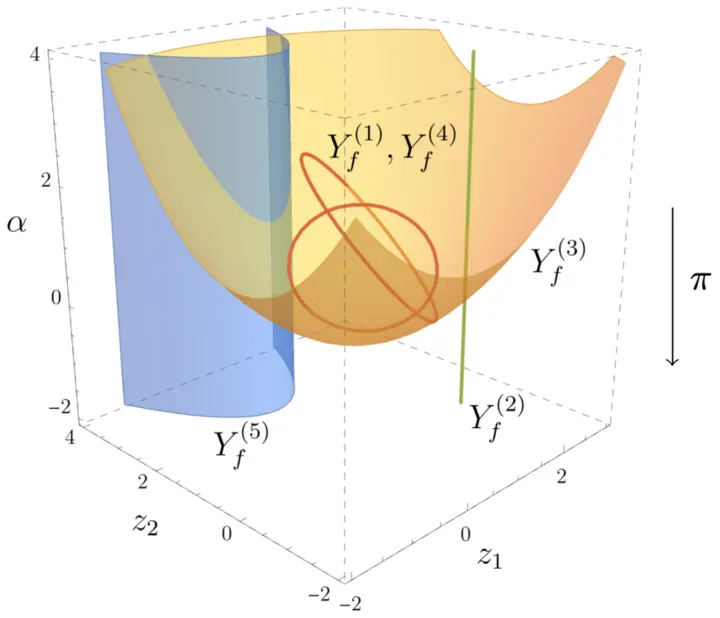
The researchers establish a novel method to constrain complicated functions that arise in the study of collisions of fundamental particles. This progress is achieved by computing geometric objects, called "Landau singularities", which encode when virtual particles become manifest in observable phenomena. The authors revisit this long-established construction from a new point of view. They use recent advanced mathematical tools involving algebra, geometry, numerical computation and topology to speed up the analysis of Landau singularities significantly. The computer program released by the authors will help physicists worldwide to study particle collisions, such as those leading to the Higgs boson production at the Large Hadron Collider.