Samantha Fairchild honored with Walter Benjamin Fellowship
Published 16.01.2023
Great news at the start of the new year comes from our postdoc Samantha Fairchild. She was awarded a two-year Walter Benjamin Fellowship of DFG (German Research Foundation) for her research on the “Analysis of discrete sets arising from geometry” – a perfect opportunity to run her own research program at our institute.
The groundbreaking nature of the project works at finding underlying connections between the seemingly disparate fields of translation surfaces and nonlinear algebra. The study of translation surfaces and their moduli spaces takes advantage of techniques coming from dynamics, number theory and geometry. Nonlinear Algebra also has broad reaching techniques, building a theory that brings algebraic geometry into a world of computations and applications. Samantha hopes this project will lead to new breakthroughs by sharing methods that are new to each respective field.
Samantha Fairchild received her PhD in mathematics from the University of Washington in 2021. Then she started her postdoc at our institute in Paul Breiding's Emmy Noether group. His mentorship was scientifically enriching, as well as helpful in developing skills for writing grants and presenting research effectively.
Take a look at the recently published paper by Paul Breiding, Samantha Fairchild, Pierpaola Santarsiero, Elima Shehu, which analyzes the expected behavior of an algebraic variety, by looking at how it intersects with random planes. The algebraic variety is used in computer vision when trying to reconstruct 3d objects from a series of images.
The second thread of Samantha’s fellowship, which focuses on analytic representations and approximation of the underlying algebraic curve, was inspired by Bernd Sturmfels. Together with Türkü Özlüm Çelik and Yelena Mandelshtam she published the paper “Crossing the transcendental divide: from translation surfaces to algebraic curves”. They coined this project “crossing the transcendental divide”. There are more ongoing projects continuing the theme of “crossing the transcendental divide”.
The Walter Benjamin Program enables researchers in the postdoctoral training phase to independently conduct their own research project at a location of their choice. The fellowship provides the salary as well as a fixed budget for scientific purposes such as attending conferences or hosting scientific visitors.
Read how Samantha Fairchild’s describes her project specifically:
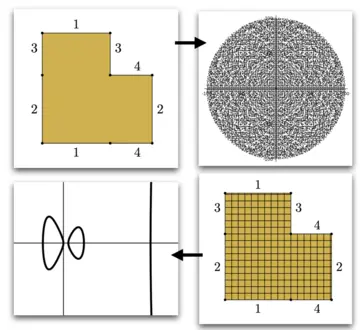
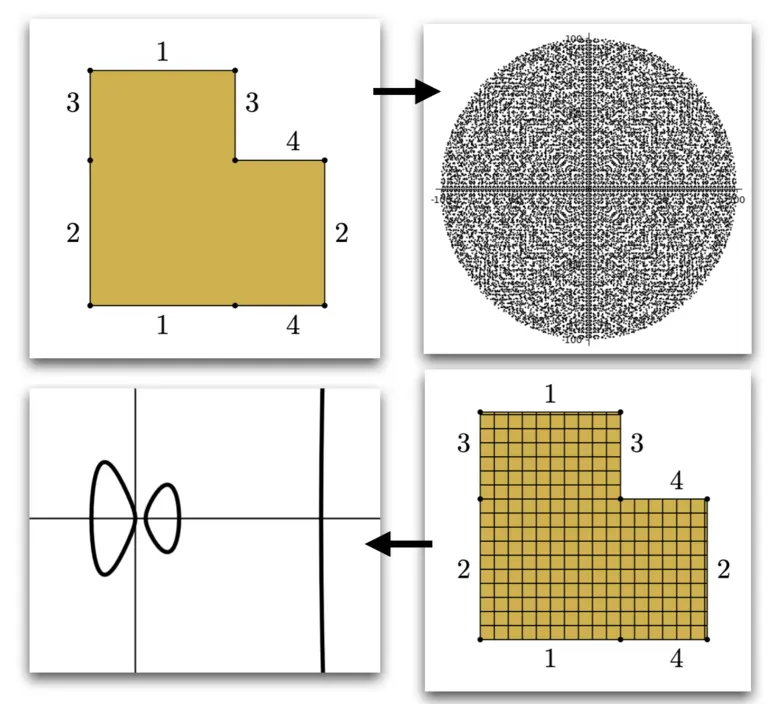
The project has two directions highlighted by the image. On the top left, we take an L shaped polygon and identify sides according to the numbering. This surface is called the Golden L, since the L shaped polygon has side lengths given by the golden ratio. By studying trajectories which start and end at the vertices of the polygon, we obtain the pattern of points on the right hand side. We analyze the symmetries of these points sets, seeing what they determine about the geometry of the Golden L. On the bottom of the picture, given the golden L, we subdivide it into finitely many smaller regions, and we can approximate the algebraic curve associated to the golden L, which is pictured on the bottom left. This is one example of using discrete information to cross the transcendental divide from analysis to algebra.
Scientific Contact
Samantha Fairchild
Editorial Contact
Discover More
-
www.dfg.de
Information on the Walter Benjamin Program