Coarsening
Gradient flow dynamics...
Coarsening dynamics are gradient flow dynamics. This means, the evolution of an out-of-equilibrium system towards relaxation follows the steepest descent in an energy landscape. In many two-phase systems, the energy is proportional to the area of the interfacial layer between these phases. Therefore, descent in an energy landscape corresponds to reduction of the interface - the pattern formed by the two phases "coarsens".
...and scaling laws
The average "size" of the one-phase components reflects the current state of ordering, which increases during the evolution. Despite the possibly complex pattern observed in the coarsening process, experimental and numerical measurements indicate that this characteristic length scale is a simple function of time: Typically, coarsening rates are power laws.
For different models from physics, we study coarsening rates using rigorous mathematical analysis. Our approach is based on the gradient flow structure of the dynamics. Our method translates information on how fast the energy density, i.e. energy normalized by system volume, decreases as a function of (geodesic) distance in the space of configurations into information on how fast the energy density decreases as a function of time. More precisely, we prove time-averaged lower bounds on the energy density. Since the energy is proportional to the interfacial area, the energy density scales like an inverse length, and thus, lower bounds on the energy density can be interpreted as upper bounds on the coarsening rate.
In the following, we illustrate bounds on coarsening rates by means of three examples: diffusion-mediated coarsening, flow-mediated coarsening, and coarsening of droplets on a thin precursor layer.
Example I: Coarsening mediated by diffusion
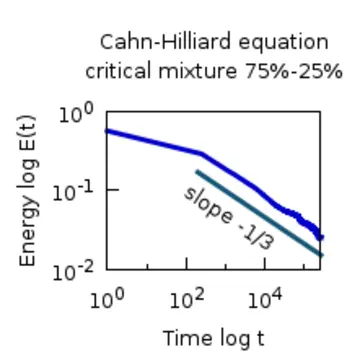
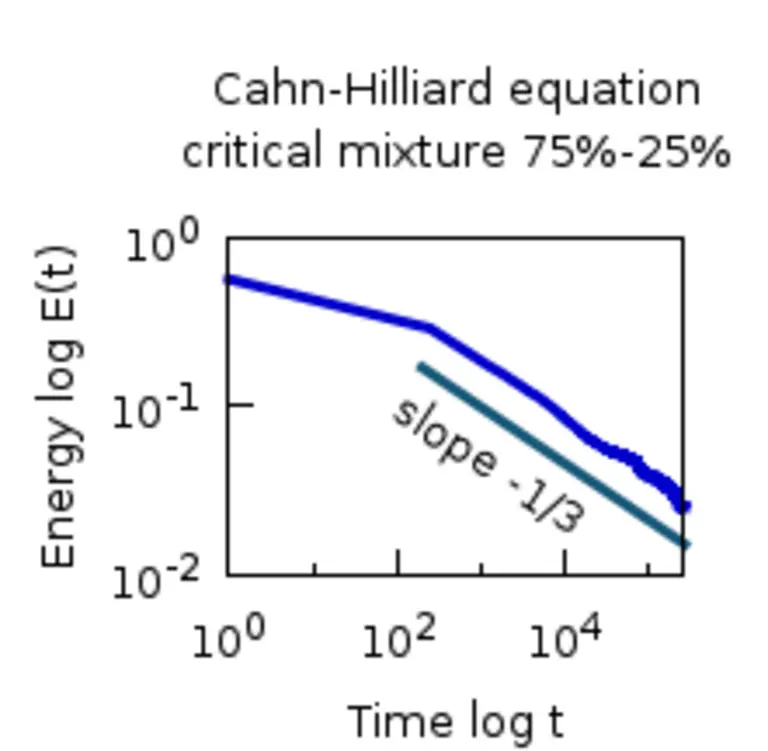
The physically most intuitive mechanism of rearrangement is diffusion, that is, the cross-motion of unlike particles. Coarsening by diffusion is observed in different systems in physics, like phase separation of metallic alloys, liquids, or polymer mixtures. Usually, the separation process preceeds a quench from a high to a low temperature. In the shallow-quench regime, i.e. temperatures close to some critical value, diffusion takes place through the bulk, i.e. the single-phase domains, whereas in the deep-quench regime, i.e. very low temperatures, diffusion takes place along the interface between the two phases. Mathematically, diffusion-mediated coarsening can be modelled by Cahn-Hilliard equations (fourth-order parabolic equations), where different mobilities reflect the different ways of diffusion: constant mobility corresponds to bulk diffusion and degenerate mobility corresponds to diffusion along the interface.
Depending on the type of diffusion, different coarsening rates are expected: If \(l(t)\) denotes the average domain size at time \(t\), these are \(l(t) \sim t^{1/3}\) for bulk diffusion and \(l(t) \sim t^{1/4}\) for diffusion along the interface. In a joint work with Robert V. Kohn [Reference 1], it has been shown that coarsening cannot proceed faster than these rates, independently from the particular choice of the initial configuration. In the case of bulk diffusion, the actual coarsening rate has a weak dependence on space dimension and volume fraction. In fact, in the regime of low volume fraction, the minor phase forms spherical and well-separated islands. During the evolution, the larger islands grow at the expense of smaller ones which eventually disappear - a phenomenon called Ostwald ripening. It turns out that in two space dimensions, the coarsening rate shows a logarithmic dependence on the volume fraction. This phenomenon has been investigated in a joint work with Sergio Conti and Barbara Niethammer [Reference 2].
Example II: Coarsening mediated by convection
In viscous liquids, e.g. in polymer mixtures, in the shallow quench regime, there is a second rearrangement mechanism besides bulk diffusion: Due to the viscosity of the liquid, particles can additionally be convected by the hydrodynamic bulk flow. The mathematical model that accounts equally for diffusion and convection is a Cahn-Hilliard equation which is coupled to a (stationary) Stokes equation.
It turns out, that in the early stages of phase separation, diffusion is the relevant coarsening mechanism. Accordingly, the coarsening rate is again \(l(t) \sim t^{1/3}\). Later on, when the average domain size has reached a certain value, a fluid flow sets in and the coarsening process is essentially driven by convection. This leads to a crossover in the coarsening rates to the much faster rate \(l(t) \sim t\). Together with Yann Brenier, Christian Seis, and Dejan Slepcev, we have investigated the coarsening rates in the convective regime [Reference 3] and the crossover from diffusion-mediated to convection-mediated coarsening [Reference 4] rigorously.
Example III: Coarsening of droplets on a thin precursor layer
Some liquids spread on a substrate form droplet configuration on a thin liquid layer. The energy of these configurations is essentially proportional to the surface area of the droplets. Therefore, since the total volume of the droplets remains constant during the evolution, energy decrease is accompanied with coarsening of the droplet pattern. Two coarsening mechanisms are relevant: collapse and collision. Droplet collapse relies on mass exchange from larger to smaller droplets through the precursor layer. This situation is very similar to the Ostwald ripening process observed for diffusion-mediated coarsening in the low-volume fraction regime, as described above: large droplets grow at the expense of small ones which eventually collapse. The basic difference between these two phenomena lies in the mixed dimensionality: Ripening of droplets of a \((d-1)\)-dimensional substrate is \(d\)-dimensional with respect to mass and energy, but \((d-1)\)-dimensional when it comes to the dynamics. As do the particles in traditional Ostwald ripening, the droplets drift. However, since the mobility of droplets depends on height, droplets are much more mobile than particles in Ostwald ripening. This effect may lead to collision and thus "accidental" coarsening.
Heuristics, numerics and experiments suggest that \(l(t) \sim t^{1/5}\) in two space dimensions and \(l(t) \sim t^{1/4}\) in three space dimensions. In joint work with Tobias Rump and Dejan Slepcev, we rigorously derive upper bounds on these coarsening rates [Reference 5]. These bounds are independent of the question whether migration or Ostwald Ripening is the dominant coarsening mechanism. The role of migration is studied by the same authors, together with Karl Glasner, in [Reference 6]. Using heuristic, asymptotic and rigorous arguments we gain the following insides: Droplets migrate in the direction of the source of the ambient flux generated by the Ostwald ripening. The migration velocity and the volume change scale with the droplet size and distance, which yield the typical time scales for migration and Ostwald ripening. In particular, it can be shown that in cases of highly mobile droplets and large average film height, the coarsening process of a droplet configuration is collision-dominated.
References
Upper bounds on coarsening rates
In: Communications in mathematical physics, 229 (2002) 3, pp. 375-395Coarsening rates in off-critical mixtures
In: SIAM journal on mathematical analysis, 37 (2006) 6, pp. 1732-1741Upper bounds on coarsening rates in demixing binary viscous liquids
In: SIAM journal on mathematical analysis, 43 (2011) 1, pp. 114-134Crossover of the coarsening rates in demixing of binary viscous liquids
In: Communications in mathematical sciences, 11 (2013) 2, pp. 441-464Coarsening rates for a droplet model : rigorous upper bounds
In: SIAM journal on mathematical analysis, 38 (2006) 2, pp. 503-529Ostwald ripening of droplets : the role of migration
In: European journal of applied mathematics, 20 (2009) 1, pp. 1-67Presentations
- General overview, among others coarsening in spinodal decomposition
(see PDF, 1.3 Mbyte) - Coarsening and Ostwald ripening in spinodal decomposition and for viscous droplets
(see PDF, 0.9 Mbyte)