Matching problem and optimal transportation
Published Aug 3, 2022
Lukas Koch
Optimal matching and optimal transportation
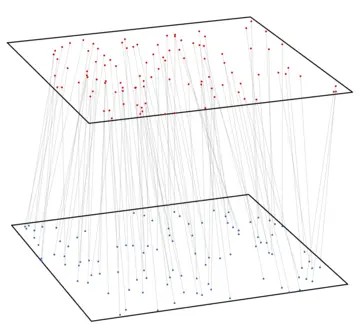
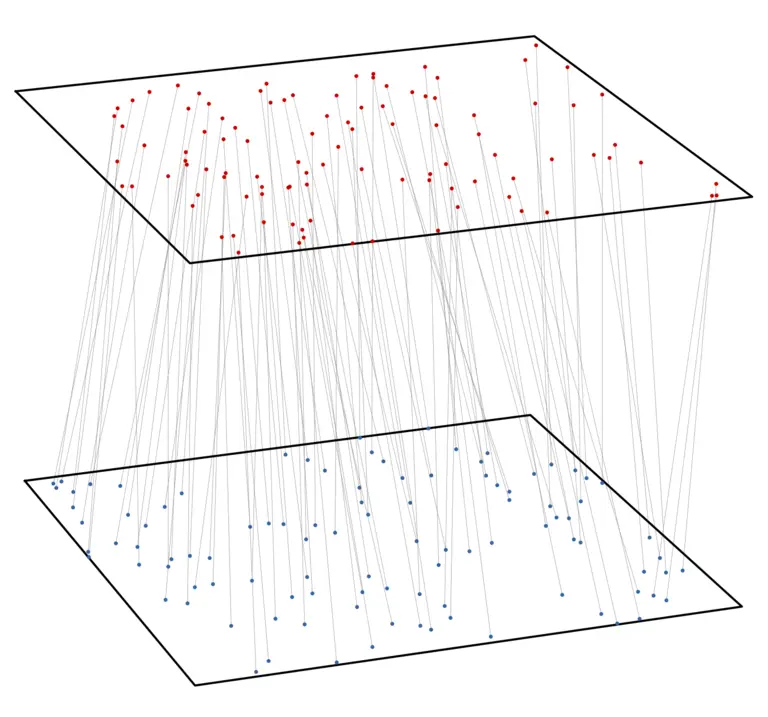
Optimal transportation describes the problem of finding the most efficient way to move a distribution of materials $\mu$ to the consumers $\lambda$, given that to move one unit of material from $x$ to $y$ costs $c(x-y)$. Since its first formulation by Monge in 1781, this problem has always been driven by applications. In fact, already its formulation was motivated by military supply considerations. Recently, the problem has generated additional interest due to applications in maschine learning and AI. A common problem in these applications is to have two sets of data points $\{x_i\}$ and $\{y_i\}$ and to seek a matching $T\colon\{x_i\}\to \{y_i\}$ that minimizes some total cost, say $\sum |x_i-y_i|^2$. This problem is known as the optimal matching problem. An illustration of such a matching, where both $\{x_i\}$ and $\{y_i\}$ are distributed according to a Poisson point process, is given in Figure 1. Note that optimal matching problems, as described, can be seen as a special case of optimal transportation problems where the original and final distributions are point measures; that is they are discrete measures.
Optimal matchings in 2d
When considering the optimal matching problem with point clouds in $\mathbb{R}^d$ that are distributed according to the Poisson point process; it is possible to see that the expected cost is infinite. This is due to the fact that the expected distance of a point $x_i$ to a point in $\{y_i\}$ is positive. Thus, it is natural to look for solutions that are 'locally' optimal, that is, they are optimal when restricted to a finite subset of points. This property is known as cyclical monotonicity since we can see it as saying that under a cyclical re-matching of a finite number of points, the cost increases. Moreover, the Poisson point process is invariant under translations. Hence, we expect the optimal matching to retain this invariance. This property is known as stationarity. However, for the quadratic cost $|x-y|^2$, cyclically monotone stationary matchings do not exist [3].
Harmonic approximation
The proof of the non-existence of stationary, locally optimal matchings in 2d is based on a tool, which is called harmonic approximation. It says that optimal transportation maps are well-approximated by harmonic maps.
The harmonic approximation result was originally developed in [2], in order to study the regularity properties of solutions to the quadratic optimal transportation problem. These problems had been studied before mainly using techniques from nonlinear PDE theory developed by Caffarelli [4,5]. The outcome of these studies was a partial $C^{1,\alpha}$-regularity theory for the transportation map, under the assumption that $\mu$ and $\lambda$ are compactly supported measures with $C^{1,\alpha}$-densities [1,6]. In [2] this result is reproven using a variational approach.
This approach relies primarily on the connection of the optimal transportation problem with a linearized PDE problem. Note that we can view an optimal transportation map $T$ as a change of variables. Thus, at least formally, we should expect the change of variables formula to hold; that is $$ \lambda(T(x))\textup{Det}\,(\nabla T(x)) = \mu(x). $$ It turns out that not only does the change of variables formula hold, but $T$ satifies a further structural restriction- $T(x)-x$ must be the gradient of a convex map! Re-writing the change of variables formula in terms of this convex function $\phi$, we obtain $$ \lambda(\nabla\phi(x)) = \textup{Det}\,(\textup{Id}+\nabla^2\phi(x)) = \mu(x). $$ The idea of the harmonic approximation is to perform a Taylor-expansion for $\textup{Det}$ around the identity. Since $\textup{Det}(\textup{Id}+A)\sim 1+ \textup{tr}\, A$, if we assume in addition that $\mu\sim\lambda\sim 1$, this gives at first order the equation $$ -\Delta\tilde \phi = \mu-\lambda. $$ If this argument is not just formal but can be made rigorous, we should expect that $\tilde \phi\approx \phi$. This is the outcome of the harmonic approximation result in [2]. We illustrate this connection in Figure 2, by comparing the averaged dislocation vector of an optimal matching (red) to the averaged gradient of a harmonic map, which is constructed according to the harmonic approximation theory.
References
| [1] | Figalli, Alessio, and Young-Heon Kim. Partial regularity of Brenier solutions of the Monge-Ampere equation. Discrete & Continuous Dynamical Systems 28.2 (2010): 559. doi: 10.3934/dcds.2010.28.559 |
| [2] | Goldman, Michael, and Felix Otto. A variational proof of partial regularity for optimal transportation maps. Annales scientifiques de l'Ecole Normale Supérieure. Vol. 53. No. 5. 2020. doi: 10.24033/asens.2444 |
| [3] | Huesmann, Martin, Francesco Mattesini, and Felix Otto. There is no stationary cyclically monotone Poisson matching in 2d. arXiv preprint arXiv:2109.13590 (2021). doi: 10.48550/arXiv.2109.13590 |
| [4] | Caffarelli, Luis A. A localization property of viscosity solutions to the Monge-Ampere equation and their strict convexity. Annals of mathematics 131.1 (1990): 129-134. doi: 10.2307/1971509 |
| [5] | Caffarelli, Luis A. The regularity of mappings with a convex potential. Journal of the American Mathematical Society 5.1 (1992): 99-104. doi: 10.2307/2152752 |
| [6] | De Philippis, Guido, and Alessio Figalli. Partial regularity for optimal transport maps. Publications mathématiques de l'IHÉS 121.1 (2015): 81-112. doi: 10.1007/s10240-014-0064-7 |