Viscous Thin Films: MPI MIS

Thin liquid films appear in a variety of situations in nature and in engineering applications. Examples include tear films in the eye, membranes in biophysics, linings in the lungs of animals, or paints. Despite the diversity of phenomena and applications, the mathematical modeling is quite similar if the film is sufficiently viscous. Excluding other contributions such as rotational forces, gravity, or van-der-Waals (molecular) interactions, it is reasonable to assume that the dynamics of the film are only driven by surface tension and viscosity, indicating the gradient-flow structure of the problem. In the regime of thin films, one commonly refers to this approach as lubrication approximation.

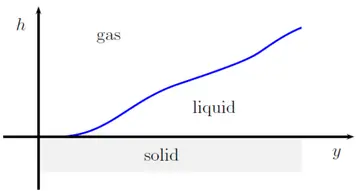
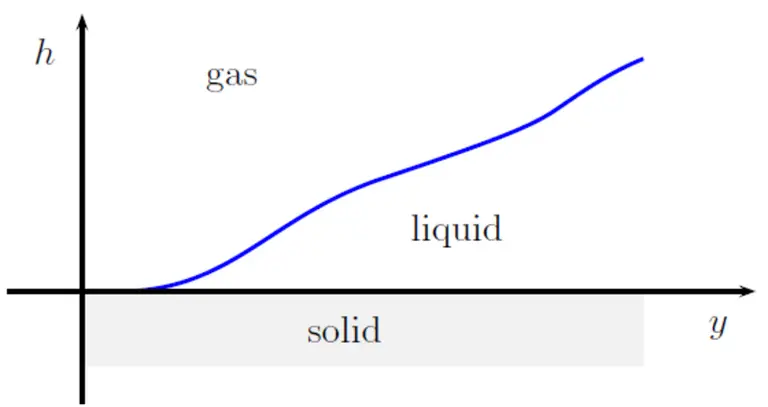
The resulting partial differential equation is a fourth-order degenerate-parabolic equation that - for a $(d + 1)$ -dimensional thin film on a $d$ -dimensional flat solid - reads

$\partial_{t} h + \nabla \cdot ((h^{3} + λ^{3 - n} h^{n}) \nabla Δ h) = 0,$ (1)

where $h = h (t, y)$ is the height of the film, $t$ the time, $λ$ the slip length, $0 < n < 3$ the mobility exponent, and $y \in R^{d}$ the lateral variable (base point). The parameters $λ$ and $n$ are determined by the underlying fluid model from which equation (1) originates: The case $λ = 0$ can be derived by an asymptotic expansion from the (Navier-) Stokes system as the underlying model, with the standard no-slip condition at the liquid-solid interface [f,m]. This model, however, leads to the well-known no-slip paradox [a-c]: A contact line (triple junction), separating the three phases (liquid, gas, and solid), can only move by inserting an infinite amount of energy into the system to overcome dissipation. This is reflected by a singularity of the solution of (1) at the boundary $\partial {h > 0}$ of the droplet and in fact the underlying Stokes system is ill-posed. One way to remove this paradox is to introduce slippage: The no-slip condition is replaced by a Navier-slip condition, where a nonzero horizontal component of the fluid velocity at the liquid-solid interface is allowed. This leads to the additive term $λ^{3 - n} h^{n}$ in the lubrication model (1).

Equation (1) is a fourth-order equation with a moving (free) boundary, that is, 3 boundary conditions are needed:

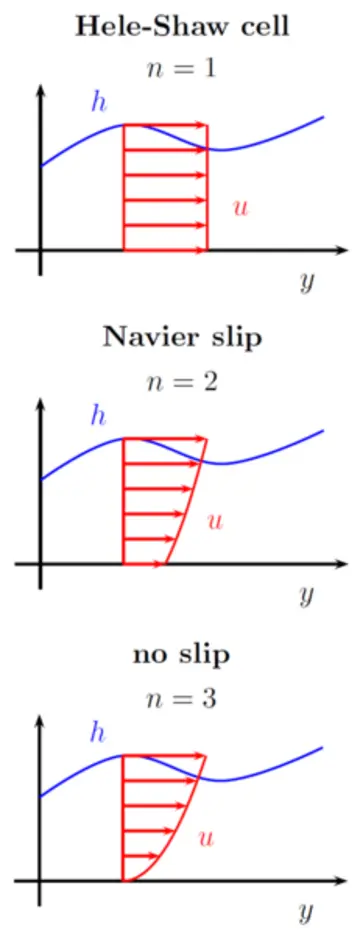
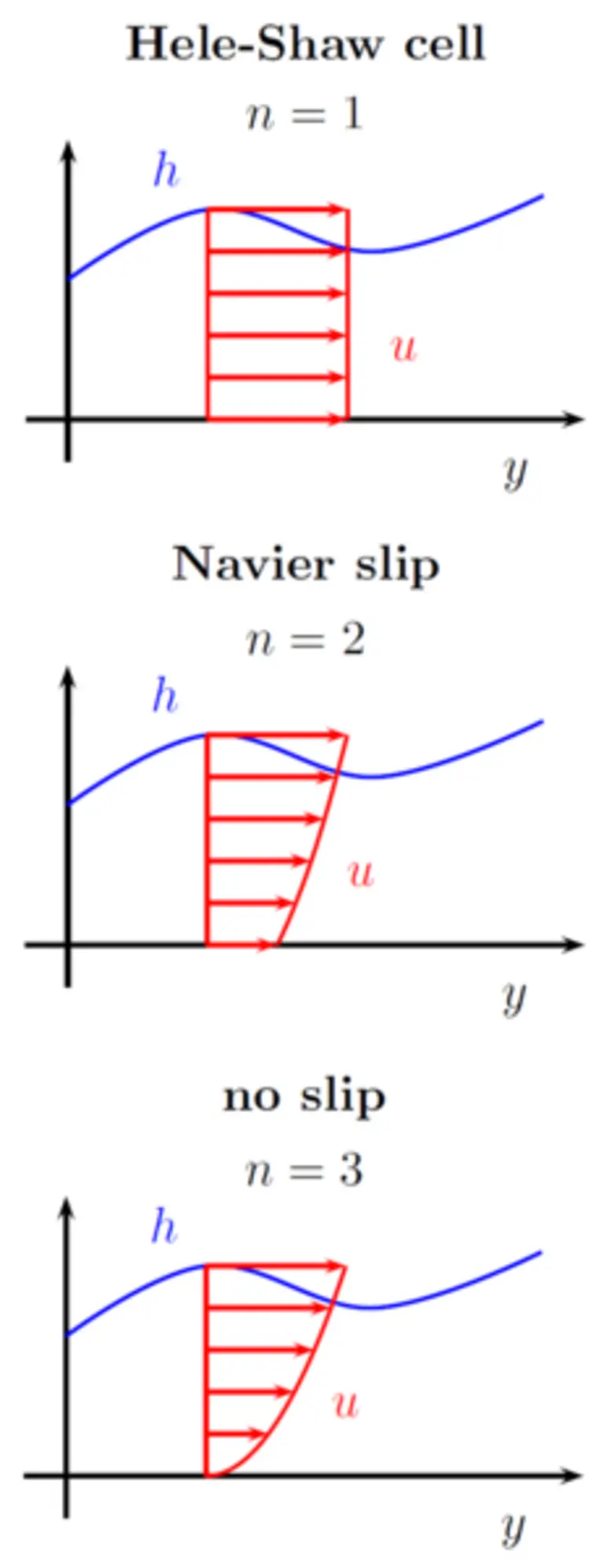
$h = 0$ at $\partial {h > 0}$ . This condition merely defines the position of $\partial {h > 0}$ .
$\partial_{ν} h = 0$ on $\partial {h > 0}$ , where $ν$ is the interior normal of $\partial {h > 0}$ . For a quasistatic evolution of the thin film, the contact angle is determined by an equilibrium of the surface tensions of the three interfaces (liquid-gas, liquid-solid, solid-gas). Assuming $\partial_{ν} h = 0$ at $\partial {h > 0}$ implies that such a local equilibrium is never attained and the film will generically not stop spreading (complete wetting regime), in contrast to the case of partial wetting, where without loss of generality $| \partial_{ν} h | = 1$ on $\partial {h > 0}$ . Finally, the simplifying assumption of a quasi-static movement can be relaxed to dynamic contact angles.
One can also view equation (1) as a continuity equation, that is, $\partial_{t} h + \nabla \cdot (V h) = 0$ in ${h > 0}$ , where the transport velocity $V$ is given by $V = (h^{2} + λ^{3 - n} h^{n - 1}) \nabla Δ h$ . By compatibility, the boundary value of $V$ on $\partial {h > 0}$ has to equal the velocity of the contact line. This condition ensures conservation of mass.

Often one assumes that the film height $h$ is small compared to the slip length $λ$ . Thus, we are lead to the study of the free boundary problem

$\partial_{t} h + \nabla \cdot (h^{n} \nabla Δ h) = 0$ for $t > 0$ and $y \in {h > 0}$ , (2a)

$h = \partial_{y} h = 0$ for $t > 0$ and $\partial {h > 0}$ , (2b)

$lim_{{h > 0} ∋ y \to \partial {h > 0}} h^{n - 1} \nabla Δ h = U (t, y)$ for $t > 0$ and $\in {h > 0}$ , (2c)

where $U (t, y)$ denotes the velocity of the free boundary $\partial {h > 0}$ .

The mathematical treatment of the thin-film equation started with the work of Bernis and Friedman [h] establishing existence of weak solutions in $d = 1$ . This approach mainly relies on the dissipation of (surface) energy $\frac{d}{d t} \int_{R^{d}} {| \nabla h |}^{2} d y = - \int_{R^{d}} h^{n} {| \nabla Δ h |}^{2} d y \leq 0$ , conservation of mass $\frac{d}{d t} \int_{R^{d}} h d y = 0$ , and a compactness argument. Further using dissipation of the "entropy" $\frac{d}{d t} \int_{R^{d}} η_{n} (h) d y = - \int_{R^{d}} (Δ h)^{2} d y \leq 0$ (where $η_{1} (h) \sim h \log h$ ), the notion of global "strong" or "entropy"

Rigorously analyzing the qualitative behavior of the contact line in solutions to the thin-film equation (2) poses significant mathematical challenges: For the porous medium equation

$\partial_{t} h = Δ h^{m}$ (3)

(with $m > 1$ ) - the second-order analogue of the thin-film equation - , estimates on free boundary propagation for weak solutions may be established by the comparison principle or Harnack inequalities. However, the thin-film equation is a degenerate parabolic equation of fourth order; thus, no comparison principle is available anymore and no Harnack inequalities are known either. For this reason, for solutions to the thin-film equation it was not even known until recently whether the free boundary would ever move near a given point on the initial free boundary. The situation was no different for other higher-order degenerate parabolic equations: No lower bounds on free boundary propagation for higher-order degenerate parabolic PDEs had been available at all. In the recent papers [8,13], we have devised a technique for the derivation of lower bounds on free boundary propagation for higher-order parabolic equations. The key ingredient of our approach are new monotonicity formulas for weak solutions to the thin-film equation of the form

$\partial_{t} \int_{R^{d}} h^{1 + α} | y - y_{0} |^{γ} d y \geq c \int_{R^{d}} h^{1 + α + n} | y - y_{0} |^{γ - 4} d y$

(for certain $α \in (- 1, 0)$ and $γ < 0$ ); these formulas are valid as as long as the support of the solution $h$ does not touch the singularity of the weight at $y_{0}$ . Combining these formulas with a differential inequality argument due to Chipot and Sideris [e], estimates from below on support propagation may be derived. By this method, we have obtained sufficient criteria for instantaneous forward motion of the free boundary, upper bounds on so-called waiting times, as well as lower bounds on asymptotic free boundary propagation rates. For $2 < n < 3$ , we have succeeded in proving that the free boundary starts moving forward instantaneously near some point $y_{0} \in \partial {h_{0} > 0}$ if the initial data $h_{0}$ grow steeper than $| y - y_{0} |^{4 / n}$ near $y_{0}$ . This is optimal since (with a grain of salt) in [s] it has been shown that growth of at most $| y - y_{0} |^{4 / n}$ entails a so-called waiting time phenomenon: The free boundary does not move beyond its initial location before some waiting time has passed. In such a case, our method yields upper bounds on the waiting time which are optimal up to a constant factor. In the borderline case $n = 2$ , we obtain upper bounds on waiting times and sufficient conditions for immediate forward motion of the interface which are optimal up to a logarithmic correction term. Interestingly, for $n < 2$ the short-time behavior of free boundaries is more complex. Again, for initial data $h_{0}$ growing at most like $| y - y_{0} |^{4 / n}$ , in [s] it has been shown that a waiting time phenomenon must occur. However, already in one spatial dimension the stationary solution $(y - y_{0})_{+}^{2}$ shows that growth of the initial data $h_{0}$ steeper than $| y - y_{0} |^{4 / n}$ does not necessarily entail instantaneous forward motion of the interface. Nevertheless, for $1 < n < 2$ we have been able to construct initial data $h_{0}$ which grow just a bit steeper than $(y - y_{0})_{+}^{4 / n}$ and for which instantaneous forward motion of the interface occurs [11]. As these initial data are bounded from above by the steady state $(y - y_{0})_{+}^{2}$ , this is a drastic example of a violation of any comparison principle and highlights an important difference to the case of second-order degenerate parabolic equations: In the case of the second-order porous medium equation (3) the initial behaviour of the free boundary is dictated by the growth of the initial data at the free boundary. For growth steeper than $(y - y_{0})_{+}^{2 / (m - 1)}$ , instantaneous forward motion happens, while a waiting time phenomenon occurs otherwise. In contrast, in the case of the thin-film equation with $1 < n < 2$ , the initial behaviour of the interface is not determined just by the growth of the initial data at the free boundary. Regarding asymptotic propagation of the free boundary, for $\frac{3}{2} < n < 3$ we are able to show that for large times the support of any solution to the thin-film equation must spread at about the same speed as the corresponding self-similar solution. More precisely, for any $t > 0$ and any $y_{s} \in supp u_{0}$ the inclusion

$B_{R (t)} (y_{s}) \subset supp u (., t)$

holds with

$R (t) := c (d, n) | | u_{0} | |_{L^{1}}^{n / (4 + n d)} t^{1 / (4 + n d)} - diam (supp u_{0})$ .

Our method for the derivation of lower bounds on free boundary propagation is not limited to the thin-film equation, but is flexible enough to be applied to other higher-order nonnegativity-preserving parabolic equations: For example, in the case of the so-called quantum drift-diffusion equation an adaption of our ansatz can be used to prove infinite speed of propagation [12].

t is well-known since [j] that the thin-film equation can be seen as the gradient flow of the surface energy with respect to a Wasserstein-type metric for all mobilities $n$ . Considering the space of functions

$N = {h : R \to [0, \infty [| \int_{R} h d y = 1}$ ,

we can think of its tangent space as

$T_{h} N = {δ h : R \to R | \int_{R} δ h d y = 0}$ .

Identifying a tangent vector $δ h \in T_{h} N$ with a solution $v$ of the equation

$δ h + \partial_{y} (v h^{n}) = 0$ ,

we define a metric tensor by

${⟨ δ h, δ h ⟩}_{h, n} := \int_{R} v^{2} h^{n} d y$ .

One observes that the gradient flow with respect to this metric and the free energy

$E_{α} (h) := \frac{1}{2} \int_{{h > 0}} {(\partial_{y} h)}^{2} d y + \frac{α}{2} | {h > 0} |$ , (4)

for $α \in {0, 1}$ leads to the thin-film equation with complete / partial wetting boundary conditions, i.e.

$| \partial_{y} h (y) | = α for y = Y (t)$ .

This insight was used to obtain a first existence result for weak solutions in the partial wetting regime [1], where an approximative time-discrete solution for time-step size $τ$ was constructed via the minimizing movement scheme

$h_{τ}^{(k)}$ is minimizer of $h \mapsto \frac{d^{2} (h_{τ}^{(k - 1)}, h)}{2 τ} + E (h)$ , (5)

which is formally equivalent to the time-discrete gradient flow equation. Here $d$ denotes the Riemannian distance induced by ${⟨ \cdot, \cdot ⟩}_{h, n}$ , which in the case $n = 1$ is known to be the well-studied Wasserstein distance. The gradient flow structure is also crucial in understanding how (2) with $n = 1$ arises as the lubrication approximation of the Darcy flow in a Hele-Shaw cell. In a first work [2] it was shown that the scheme (5) can be seen as the $Γ$ -limit of the suitably rescaled corresponding discrete schemes of the Hele-Shaw flows. The lubrication approximation for the full equation was then made rigorous in the complete wetting case in [4], using one of the main insights from [2] that the contact angle is a consequence of an instantaneous energy relaxation at the triple point rather than an imposed contraint. The energy landscape described by $E$ and ${⟨ \cdot, \cdot ⟩}_{h, n}$ is globally non-convex. Nevertheless, in the partial wetting case with linear mobility it is convex in a region close to the stationary solution $(x)_{+}$ , an observation which leads to natural relaxation rates of perturbations of the stationary solution [16]. Including intermolecular forces in the energy (4) in the form of a potential $U$ leads to a phenomenon where a configuration of droplets coarsens. This means that the number of droplets decreases, while the average size of single droplets increases. The rates by which this happens are investigated in [5,7], for a more detailed discussion, please see the related page on coarsening.

It appears natural to ask whether the introduction of slippage indeed removes the singular behavior at the contact line. This leads to the mathematical question of regularity of the solution at the free boundary. In fact, developing a regularity theory for degenerate-parabolic fourth-order equations is a relatively new field. For the thin-film problem (2) we refer to the works of Giacomelli, Knüpfer, and two of the group members [6,10,v,y,z], in particular addressing the case of $n = 1$ in the complete wetting regime. Here the solution is in fact smooth up to the contact line. However, such qualitative behavior cannot be expected for other mobility exponents as first noticed by Knüpfer in the partial wetting case and $d = 1$ [w,x]. One of the ongoing projects of our group is to understand the case of complete wetting, where a moving contact line is the generic situation.

Apart from the applied point of view, there is also a theoretical interest in the questions detailed above, since before the analysis starting with [6], uniqueness results have not been available for (2). The existence results for weak solutions [h,i,k,o,q] always relied on a compactness argument since the control of the solutions at the free boundary was not strong enough to apply the contraction mapping theorem. Again it is the detailed understanding of the regularity at the free boundary that enables us to prove existence and uniqueness of solutions for short times or for initial data close to generic solutions (stationary, traveling waves, or self-similar solutions, see below).

There is another theoretical motivation for our analysis, coming from the porous medium equation (3). Here a well-developed existence and uniqueness theory is available [g,p,r], which, however, at least partially relies on the use of a maximum (or comparison) principle. Therefore it seems of interest to study which of the analysis does or does not transfer from the second-order to the fourth-order case. Although the works for the particular case $n = 1$ [6,10,v] support the claim that the analysis does transfer, this is not true for all other mobility exponents. Only for $n = 1$ the partial differential operator of a suitable linearization turns out to be the square of the well-understood linearized porous-medium operator.

It is instructive to further simplify the problem (2) to the case in which the behavior of solutions is self-similar. This is in fact the generic large-time behavior of solutions with compact support [15,t]. Here, the PDE problem (2) reduces to the study of a boundary-value problem for a third-order nonlinear ODE. Jointly with Lorenzo Giacomelli, we are able to show that the solution is generically not smooth, even if the leading-order traveling wave is factored off [9]. Instead we are able to prove analyticity in two variables: Factoring off the traveling-wave profile, the solution is an analytic function in $(x, x^{β})$ , where $x$ denotes the distance to the boundary and $β$ is an in general irrational number. $1$ and $β$ are in fact the eigenvalues at a hyperbolic stationary point (corresponding to the contact line) of a suitably chosen dynamical system and characterize the invariant manifold on which the solution lies. For the porous medium equation, in comparison, this invariant manifold is just one-dimensional with the trivial eigenvalue $1$ . Essentially, it is a coincidence that for $n = 1$ the two eigenvalues in the thin-film case coincide.

Given the understanding for the source-type solution, we can also treat the general PDE problem (2) for the physical relevant case of quadratic mobility ( $n = 2$ ) [14]. This work is joint with Lorenzo Giacomelli and Hans Knüpfer. Here we are able to prove well-posedness of the problem for initial data that are close to the generic solution, a traveling wave $\sim x^{3 / 2}$ . Our method relies on maximal regularity estimates in weighted $L^{2}$ -spaces and a suitable subtraction of the leading-order singular expansion of the solution at the free boundary. While our method yields a well-posedness result, the question of higher regularity is of ongoing interest and will be adressed in future work. Furthermore, we are also interested in generalizing our result (which is in fact valid for an interval of $n$ around $n = 2$ ) to the full range of mobility exponents $n \in (0, 3) .$

Currently our main interest lies in a deeper understanding of the full system including slippage, for which source-type self-similar solutions do not exist. Thus even simplified ODE models turn out to be mathematically subtle. In particular the traveling-wave solution has no explicit characterization and exhibits two asymptotic regimes. Close to the contact line the solution has a similar asymptotic expansion as the source-type self-similar solution in the scaling-invariant case (2), whereas in the interior of the droplet we observe another asymptotic regime known as Tanner's law [d,l]. Here we are able to show that Tanner's solution (which was found in the case of no-slip, i.e. $λ = 0$ ) is affected by the microscopic physics only in higher order corrections [17]. Furthermore, continuous (smooth) variations of the microscopic model (by e.g. varying the mobility exponent $n$ ) lead to continuous (smooth) variations of these corrections. This work is closely related to an earlier work of Giacomelli and one of the group members [3], where it is shown that the effect of slippage affects the spreading rate of the droplet only by a logarithmic correction. The proof relies on the gradient flow structure of the thin-film equation by monitoring three physical integrals: the free energy, the dissipation, and the length of the apparent support.

In future work we would like to investigate the lubrication approximation starting from solutions of the (Navier-) Stokes system with slippage. Such a rigorous lubrication approximation was indeed carried out by Giacomelli and one of the group members in earlier work for the particular case $n = 1$ using weak solutions [2,4]. Here problem (2) can be understood as the lubrication approximation of the Darcy flow in the Hele-Shaw cell (see also [y,z] for the partial wetting case and classical solutions). We expect that this problem is mathematically challenging and would like to understand it first at a simplified level, that is, by studying traveling-wave solutions for the Stokes system and proving the lubrication limit in the steady-state case.

H. K. Moffatt. Viscous and resistive eddies near a sharp corner. Journal of Fluid Mechanics, 18:1–18, 1 1964.

Chun Huh and LE Scriven. Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. Journal of Colloid and Interface Science, 35(1):85–101, 1971.

Elizabeth B. Dussan V. and Stephen H. Davis. On the motion of a fluid-fluid interface along a solid surface. Journal of Fluid Mechanics, 65:71–95, 8 1974.

L H Tanner. The spreading of silicone oil drops on horizontal surfaces. Journal of Physics D: Applied Physics, 12(9):1473, 1979.

Michel Chipot and Thomas Sideris. An upper bound for the waiting time for nonlinear degenerate parabolic equations. Trans. Amer. Math. Soc., 288(1):423–427, 1985.

P. G. de Gennes. Wetting: statics and dynamics. Rev. Mod. Phys., 57:827–863, Jul 1985.

Sigurd Angenent. Local existence and regularity for a class of degenerate parabolic equations. Math. Ann., 280(3):465–482, 1988.

Francisco Bernis and Avner Friedman. Higher order nonlinear degenerate parabolic equations. J. Differential Equations, 83(1):179–206, 1990.

Elena Beretta, Michiel Bertsch, and Roberta Dal Passo. Nonnegative solutions of a fourth-order nonlinear degenerate parabolic equation. Arch. Rational Mech. Anal., 129(2):175–200, 1995.

R. Almgren. Singularity formation in Hele-Shaw bubbles. Phys. Fluids, 8(2):344–352, 1996.

A. L. Bertozzi and M. Pugh. The lubrication approximation for thin viscous films: regularity and long-time behavior of weak solutions. Comm. Pure Appl. Math., 49(2):85–123, 1996.

B.R. Duffy and S.K. Wilson. A third-order differential equation arising in thin-film flows and relevant to tanner’s law. Applied Mathematics Letters, 10(3):63 – 68, 1997.

Alexander Oron, Stephen H. Davis, and S. George Bankoff. Long-scale evolution of thin liquid films. Rev. Mod. Phys., 69:931–980, Jul 1997.

Michiel Bertsch, Roberta Dal Passo, Harald Garcke, and Günther Grün. The thin viscous flow equation in higher space dimensions. Adv. Differential Equations, 3(3):417–440, 1998.

Roberta Dal Passo, Harald Garcke, and Günther Grün. On a fourth-order degenerate parabolic equation: global entropy estimates, existence, and qualitative behavior of solutions. SIAM J. Math. Anal., 29(2):321–342 (electronic), 1998.

P. Daskalopoulos and R. Hamilton. Regularity of the free boundary for the porous medium equation. J. Amer. Math. Soc., 11(4):899–965, 1998.

Roberta Dal Passo and Harald Garcke. Solutions of a fourth order degenerate parabolic equation with weak initial trace. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4), 28(1):153–181, 1999.

Herbert Koch. Non-Euclidean singular intergrals and the porous medium equation. Habilitation thesis, Ruprecht-Karls-Universität Heidelberg, 1999.

Roberta Dal Passo, Lorenzo Giacomelli, and Günther Grün. A waiting time phenomenon for thin film equations. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4), 30(2):437–463, 2001.

J. A. Carrillo and G. Toscani. Long-time asymptotics for strong solutions of the thin film equation. Comm. Math. Phys., 225(3):551–571, 2002.

Roberta Dal Passo, Lorenzo Giacomelli, and Günther Grün. Waiting time phenomena for degenerate parabolic equations - a unifying approach. In Geometric analysis and nonlinear partial differential equations, pages 637–648. Springer, Berlin, 2003.

Lorenzo Giacomelli and Hans Knüpfer. A free boundary problem of fourth order: classical solutions in weighted Hölder spaces. Comm. Partial Differential Equations, 35(11):2059–2091, 2010.

Hans Knüpfer. Well-posedness for the Navier slip thin-film equation in the case of partial wetting. Comm. Pure Appl. Math., 64(9):1263–1296, 2011.

Hans Knüpfer. Well-posedness for a class of thin-film equations with general mobility in the regime of partial wetting. preprint, 2012.

Hans Knüpfer and Nader Masmoudi. Darcy flow on a plate with prescribed contact angle - well-posedness and lubrication approximation. preprint, 2012.

Hans Knüpfer and Nader Masmoudi. Well-posedness and uniform bounds for a nonlocal third order evolution operator on an infinite wedge. Comm. Math. Phys., 320(2):395–424, 2013.

Logarithmic correction to droplet spreading rate because of Navier slip regularization (see PS, 222 Kbyte)
Short-time existence theory of smooth solutions based on linear theory (see PDF, 1.1 Mbyte)
Towards a regularity theory for the moving contact line (see PDF, 289 Kbyte)

Figure 1: Schematic plot of a liquid thin film

Figure 2: Schematic plots of the flow fields u close to the boundary for different n.

Viscous Thin Films

Lubrication theory

The thin-film equation

The thin-film equation as a free boundary problem

Weak solutions

Qualitative behavior of the free boundary

Gradient Flow structure of the thin-film equation

Well-posedness and regularity for the thin-film free-boundary problem

Selected group publications

Lubrication approximation with prescribed nonzero contact angle

Variational formulation for the lubrication approximation of the Hele-Shaw flow

Droplet spreading : intermediate scaling law by PDE methods

Rigorous lubrication approximation

Coarsening rates for a droplet model : rigorous upper bounds

Smooth zero-contact-angle solutions to a thin-film equation around the steady state

Ostwald ripening of droplets : the role of migration

Optimal lower bounds on asymptotic support propagation rates for the thin-film equation

Regularity of source-type solutions to the thin-film equation with zero contact angle and mobility exponent between 3/2 and 3

On uniqueness of weak solutions for the thin-film equation

Behaviour of free boundaries in thin-film flow : the regime of strong slippage and the regime of very weak slippage

Infinite speed of support propagation for the Derrida-Lebowitz-Speer-Spohn equation and quantum drift-diffusion models

Upper bounds on waiting times for the thin-film equation : the Case of weak slippage

Well-posedness for the Navier-Slip thin-film equation in the case of complete wetting

Well-posedness and self-similar asymptotics for a thin-film equation

Relaxation rates for a perturbation of a stationary solution to the thin-film equation

Rigorous asymptotics of traveling-wave solutions to the thin-film equation and Tanner's law

References

Presentations

Elias Esselborn

Julian Fischer

Manuel V. Gnann