Stochastic Homogenization
Homogenization and the need for quantitative methods
Many applications, such as porous media or composite materials, involve heterogeneous media described by partial differential equations with coefficients that randomly vary on a small scale. On macroscopic scales (large compared to the dimension of the heterogeneities) such media often show an effective behavior. Typically that behavior is simpler, since the complicated, random small scale structure of the media averages out on large scales, and in many cases the effective behavior can be described by a deterministic, macroscopic model with constant coefficients. This process of averaging is called homogenization. Mathematically, it means that the replacement of the original random equation by one with certain constant, deterministic coefficients is a valid approximation in the limit when the ratio between macro- and microscale tends to infinity. A qualitative homogenization result typically states that the solution of the initial model converges to the solution of the macro model, and provides a characterization of the macro model, e. g. by a homogenization formula for the homogenized coefficients.
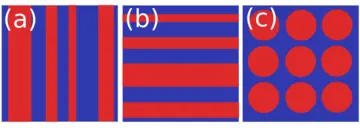
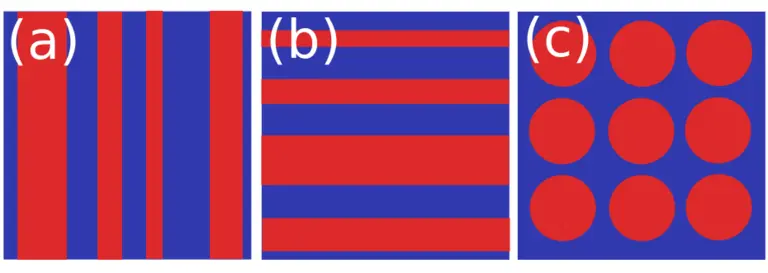
The relation between the microscopic properties of the medium and its effective ones is subtle. Figure 1 shows an example of a two-phase medium: the effective behavior not only depends on the volume fraction of the phases - it is highly sensitive to the geometry and spatial arrangement of the phases.
A qualitative homogenization result, as described above, is the starting point for a precise understanding of effective properties: it provides the object to analyze - the formula for the homogenized coefficients. However, in all non trivial cases the homogenization formula cannot be studied directly and one has to appeal to approximations. Therefore, it is an important and natural task to construct approximation schemes and to develop precise quantitative methods to evaluate their quality.
In a series of papers we investigated such questions in one of the simplest situations, namely for effective heat conduction in random media. You'll find a German language general audience introduction into partical aspects of our work under [Reference 8].
Effective heat conduction in random media
Kozlov [Koz1979], Papanicolaou and Varadhan [Pap1979] studied (steady) heat conduction in a randomly inhomogeneous conducting medium and obtained a qualitative homogenization result for stationary, ergodic conductivities. Kozlov [Koz1987] and Künnemann [Kue1983] considered the analogue problem in a discrete setting, namely for diffusion on the lattice
In the formula.
The homogenization formula involves a corrector function
Despite its simplicity, the homogenization formula has to be approximated in practice, since (2) has to be solved
- on the whole lattice
- or almost every realization of the coefficients
How to approximate the effective conductivity?
A natural answer is guided by the following observations:
- By ergodicity the ensemble average in (1) can be replaced by the spatial average
Notice that (3) only involves a single realization of the coefficients. - For stationary and periodic coefficients the infinite domain
The periodic approximation procedure exploits both observations. It consists of two steps:
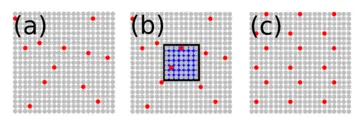
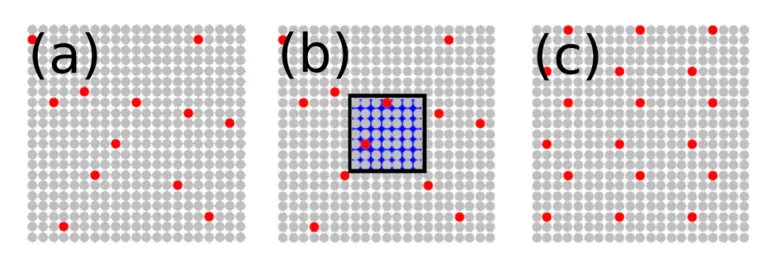
- In a first periodization step,
- Secondly, a periodic proxy
The resulting periodic proxy is a random matrix - it is in general non-deterministic, since periodization typically destroys ergodicity. However, we expect that the periodic proxy converges to the homogenized coefficients for
Quantitative Analysis
In the series of articles [Reference 2] - [Reference 4] we developed quantitative methods that allow to estimate approximation errors. By now, we have a complete picture of the periodic approximation procedure in the case of a discrete medium and independent identically distributed random coefficients, and partial results for correlated coefficients. In particular in [Reference 4], we show that the overall approximation error for i.i.d. coefficients decays with the rate of the central limit theorem, i.e.
where
Decomposition of the approximation error.
In [Reference 2] we introduced a natural decomposition of the approximation error in
- a random error - the variance of the periodic proxy,
- a systematic error - the distance of
The random error monitors the fluctuation of the periodic proxy around its average and originates in the lack of ergodicity of the L-periodic ensemble. In [Reference 2] for i.i.d. coefficients and in [Reference 4] for more general statistics, we prove that the random error has the critical scaling
The systematic error is analyzed in [Reference 3] and [Reference 4]. We observe that the systematic error is of lower order and decays almost double as fast as the random error.
Empirical averaging and the size of the representative volume element.
An interesting difference between the random and systematic error is the following: in contrast to the systematic error, the random error can be reduced by empirical averaging, i.e. by computing the periodic proxy for
Elements of our method
In the following we briefly describe some ingredients and ideas of our method.
Spectral gap on Glauber dynamics
The statistics that we consider satisfy a spectral gap estimate - a Poincaré inequality in
As in the seminal papers [Koz1979] and [Pap1979], stationarity allows to represent PDEs stated in physical space, such as the corrector problem (2), by equations in probability space. Based on that observation, we represent the corrector (and its gradient) by means of a parabolic equation in probability space.
Higher moments of the corrector
A main achievement of our analysis are estimates on higher moments of the corrector. We prove that any finite moment of the
Estimates on Green's functions
A central ingredient to quantify the decay of the mentioned parabolic equation are estimates on the parabolic Green's function which only depend on the ellipticity ratio of the coefficients. Our estimates are pointwise in time and weighted in space. They are obtained in [Reference 2] and [Reference 4] by appealing to elliptic and parabolic regularity theory.
Regularization and spectral exponents
In order to estimate certain contributions of the systematic error, we regularize the corrector equation (2) by adding a lower order term. Such a regularization is already utilized in the qualitative analysis in [Koz1979], [Pap1979]. In [Glo] it is shown that the error due to regularization is related to the spectral exponents of the elliptic operator that appears in the corrector equation. Optimal estimates on the spectral exponents for small dimensions are derived in [Reference 3] and [Glo]. As shown in [Reference 4], our quantitative methods yield optimal estimates on the spectral exponents in any dimension.
A regularity theory
Motivated by the work of Armstrong and Smart [AS], we have recently focused on questions of regularity for random elliptic operators [Reference 12]. Following the philosophy of Avellaneda and Lin [AL], who in the periodic homogenization lifted the regularity theory of the homogenized limit to the heterogeneous situation, we obtain
The proof of the
In our error estimates we only require that the generalized corrector
Using a duality argument borrowed from Avellaneda and Lin [AL], the work [Reference 12] implies estimates for the Green's function and its first and second derivative with optimal scaling away from the diagonal [Reference 18]. As a consequence of [Reference 16], where under a stronger assumption on the growth of the corrector we study the homogenization error for the solution of the equation with a compactly supported right-hand side, we obtain
Further results
Appealing to the De Giorgi-Nash-Moser theory for scalar equations, in [Reference 11] we showed the existence of and obtained estimates for the corrector together with the optimal estimates on the random and systematic error. In the periodic setting and for systems, we estimated moments of the gradient of the corrector which we then used to obtain optimal bounds for the random error [Reference 19]. Some of the methods used in [Reference 19] we borrowed from [Reference 10], where the corrector itself (in the case of a single equation) is estimated. The fluctuations of the corrector around its mean were studied in [Reference 14], where we used the Helffer-Sjöstrand transformation to identify its correlation structure. Finally, in [Reference 9] we relaxed the assumption of uniform ellipticity by considering a toy model for percolation in
Recently, for the case of coefficient fields with finite range of dependence, we combined parabolic approach and several ideas from our previous works [References 4, Reference 16] to obtain bounds on the corrector, which are near optimal in the scaling and optimal in stochastic integrability [Reference 1].
References
The corrector in stochastic homogenization : optimal rates, stochastic integrability, and fluctuations
An optimal variance estimate in stochastic homogenization of discrete elliptic equations
In: The annals of probability, 39 (2011) 3, pp. 779-856An optimal error estimate in stochastic homogenization of discrete elliptic equations
In: The annals of applied probability, 22 (2012) 1, pp. 1-28Quantification of ergodicity in stochastic homogenization : optimal bounds via spectral gap on Glauber dynamics
In: Inventiones mathematicae, 199 (2015) 2, pp. 455-515Quantification of ergodicity in stochastic homogenization: optimal bounds via spectral gap on Glauber dynamics --- long version
Annealed estimates on the Green function
In: Probability theory and related fields, 163 (2014) 3-4, pp. 527-573On annealed elliptic Green's function estimates
In: Mathematica bohemica, 140 (2015) 4, pp. 489-506Effektive Beschreibung von heterogenen Medien
In: Jahrbuch der Max-Planck-Gesellschaft, 2014 (2014), Forschungsbericht - Max-Planck-Institut für Mathematik in den NaturwissenschaftenMoment bounds for the corrector in stochastic homogenization of a percolation model
In: Electronic journal of probability, 20 (2015), p. 106Quantitative estimates on the periodic approximation of the corrector in stochastic homogenization
In: ESAIM / Proceedings, 48 (2015), pp. 80-97Quantitative results on the corrector equation in stochastic homogenization
In: Journal of the European Mathematical Society, 19 (2017) 11, pp. 3489-3548A regularity theory for random elliptic operators
In: Milan journal of mathematics, 88 (2020) 1, pp. 99-170An optimal quantitative two-scale expansion in stochastic homogenization of discrete elliptic equations
In: ESAIM / Mathematical modelling and numerical analysis, 48 (2014) 2, pp. 325-346Correlation structure of the corrector in stochastic homogenization
In: The annals of probability, 44 (2016) 5, pp. 3207-3233A higher-order large-scale regularity theory for random elliptic operators
In: Communications in partial differential equations, 41 (2016) 7, pp. 1108-1148Quantitative stochastic homogenization : local control of homogenization error through corrector
In: Mathematics and materials / Mark J. Bowick... (eds.)Providence, RI : American mathematical society, 2017. - pp. 301-327
(IAS/Park City mathematics series ; 23)
Green's function for elliptic systems : existence and Delmotte-Deuschel bounds
In: Calculus of variations and partial differential equations, 56 (2017) 6, p. 163Green's function for elliptic systems : moment bounds
In: Networks and heterogeneous media, 13 (2018) 1, pp. 155-176Corrector estimates for elliptic systems with random periodic coefficients
In: Multiscale modeling and simulation, 14 (2016) 4, pp. 1434-1462Hölder regularity for a non-linear parabolic equation driven by space-time white noise
More references:
- S. Armstrong and C. Smart. [AS]
Quantitative stochastic homogenization of convex integral functionals.
2014.
Arxiv Preprint: arxiv.org/abs/1406.0996 - M. Avellaneda and F.-H. Lin. [AL]
Compactness methods in the theory of homogenization.
Comm. Pure and Applied Math., 40(6):803--847, 1987. - A. Gloria and J.-C. Mourrat. [Glo]
Spectral measure and approximation of homogenized coefficients.
To appear in Probab. Theory Related Fields. - S.M. Kozlov. [Koz1979]
The averaging of random operators.
Mat. Sb. (N.S.), 109(151)(2):188202, 327, 1979. - S.M. Kozlov. [Koz1987]
Averaging of difference schemes.
Math. USSR Sbornik, 57(2):351369, 1987. - R. Künnemann. [Kue1983]
The diffusion limit for reversible jump processes on
Commun. Math. Phys., 90:2768, 1983. - G.C. Papanicolaou and S.R.S. Varadhan. [Pap1979]
Boundary value problems with rapidly oscillating random coefficients.
In Random fields, Vol. I, II (Esztergom, 1979), volume 27 of Colloq. Math. Soc. Janos Bolyai, pages 835873. North-Holland, Amsterdam, 1981.
Presentations
- Error bounds in stochastic homogenization (see PDF, 2.4 Mbyte)